Fiche de cours
Loi binomiale
Les conditions de la loi binomiale :
On considère une expérience aléatoire qui ne comporte que deux résultats :
- Le succès $S$ et
- l'échec $\overline{S}$ son événement contraire.
On pose :
$p=p(S)$
et $q=p(\overline{S}) =1-p(S)$
On répète $n$ fois l'expérience, les répétitions sont indépendantes.
Soit $X$ le nombre de succès au cours des $n$ répétitions.
On dit alors que $X$ suit la loi binomiale de paramètres $n$ et $p$.
On note cette loi $\mathcal{B}(n,p)$.
Exemple d'arbre pour $n=2$
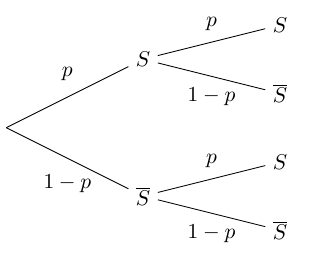
La probabilité d'obtenir $k$ succès au cours des $n$ répétitions est donnée par la formule :
$p(X=k)= \displaystyle\binom{n}{k} p^k \times (1-p)^{n-k}$
Exemple
a) On lance 10 fois un dé bien équilibré. Quelle est la probabilité d'obtenir 4 fois le chiffre 1 au cours des 10 lancers
b) Quelle est la probabilité d'obtenir au moins une fois le chiffre 1 au cours des 10 lancers ?
a) D'après la calculat
