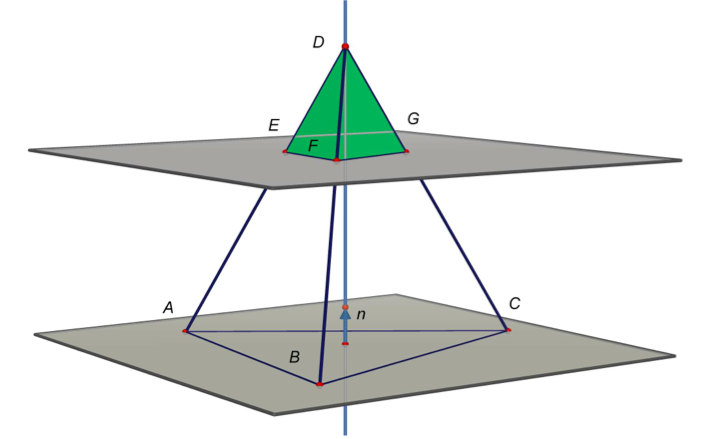
L'énoncé
L'espace est muni d'un repère orthonormal \((O; \overrightarrow{i}; \overrightarrow{j}; \overrightarrow{k})\).
Question 1
Partie A Restitution organisée de connaissances
Soit \(D\) le point de coordonnées \((x_D, y_D, z_D)\) et \(P\) le plan d'équation \(a x + b y + c z + d = 0\), où \(a\), \(b\) et \(c\) sont des réels qui ne sont pas tous nuls.
Démontrer que la distance du point \(D\) au plan \(P\) est donnée par : \(d (D,P) = \dfrac{|ax_D+by_D+cz_D+d|}{\sqrt{a^2+b^2+c^2}}\)
\(\overrightarrow{n}(a ; b ; c)\) est un vecteur normal au plan \((P)\).
Soit \(H\) la projection orthogonale de \(D\) sur \((P)\).
\((DH)\) a pour vecteur directeur \(\overrightarrow{n}\) donc il existe un réel \(k\) tel que \(\overrightarrow{DH} = k \overrightarrow{n}\).
La distance de \(D\) au plan \((P)\) est égale à \(DH\) donc à \(| k | \times ||\overrightarrow{n}||\), il suffit donc de connaître \(k\).
\(\overrightarrow{DH} = k\overrightarrow{n} \Leftrightarrow \left\{ \begin{array}{left} x_H - x_D = ka\\ y_H - y_D = kb\\ z_H - z_D = kc\\ \end{array}\right. \Leftrightarrow \left\{ \begin{array}{left} x_H = x_D + ka\\ y_H = y_D + kb\\ z_H = z_D+kc\\ \end{array}\right.\)
\(H\in (P)\) donc \(ax_H+by_H+cz_H+d=0\), soit
\(a(x_D+ka)+b(y_D+kb)+c(z_D+kc)+d=0\)
\(k (a^2 + b^2 + c^2 ) = -(ax_D+ b y_D + c z_D + d)\)
On isole $k$ :
\(k = -\dfrac{ax_D+ b y_D + c z_D + d}{a^2 + b^2 + c^2}\)
Finalement, \(DH = |k| \times ||\overrightarrow{n}||\) et
\(DH = \dfrac{\vert ax_D+ b y_D + c z_D + d\vert }{a^2 + b^2 + c^2} \times \sqrt{a^2 + b^2 + c^2}\)
Conclusion :
\(DH = \dfrac{\vert ax_D+ b y_D + c z_D + d\vert}{\sqrt{a^2 + b^2 + c^2}}\)
Faites une figure. Notez $H$ le projeté orthogonal de \(D\).
Exprimez le fait que les vecteurs \(\overrightarrow{DH}\) et \(\overrightarrow{n}\) sont colinéaires.
La longueur cherchée est \(DH\).
Question 2
Partie B
On considère les points \(A(3 ; - 2 ; 2)\), \(B(6 ; - 2 ; - 1)\), \(C(6 ; 1 ; 5)\) et \(D(4 ; 0 ; - 1)\).
1. Démontrer que le triangle \(ABC\) est rectangle. En déduire l'aire du triangle \(ABC\).
\(\overrightarrow{AB}\) a pour coordonnées \((3 ; 0 ; -3)\) donc \(AB^2 = 3^2 + 0^2 + ( -3)^2 = 18\)
donc \(AB = 3\sqrt{2}\)
\(\overrightarrow{AC}\) a pour coordonnées \((3 ; 3 ; 3)\) donc \(AC^2 = 3^2 + 3^2 + 3^2 = 27\)
donc \(AC = 3\sqrt{3}\)
\(\overrightarrow{BC}\) a pour coordonnées \((0 ; 3 ; 6)\) donc \(BC^2 = 0^2 + 3^2 + 6^2 = 45\)
Il apparait que \(AB^2 + AC^2 = BC^2\) donc d'après la réciproque de Pythagore, le triangle \(ABC\) est rectangle en \(A\). Son aire est égale à :
\(A_{ABC}=\dfrac{1}{2} AB \times AC = \dfrac{9\sqrt{6}}{2}\) u.a.
Pensez à la réciproque d’un théorème vue en 4ème.
Pythagore bien sûr… calculez les carrés des trois longueurs du triangle.
Question 3
Vérifier que le vecteur \(\overrightarrow{n}(1 ; -2 ; 1)\) est normal au plan \((ABC)\). En déduire une équation cartésienne du plan \((ABC)\).
\(\overrightarrow{n}.\overrightarrow{AB} = 1 \times 3 + ( -2) \times 0 + 1 \times ( -3) = 0\) donc les vecteurs \(\overrightarrow{n}\) et \(\overrightarrow{AB}\) sont orthogonaux.
\(\overrightarrow{n}.\overrightarrow{AC} = 1 \times 3 + ( -2) \times 3 + 1 \times 3 = 0\) donc les vecteurs \(\overrightarrow{n}\) et \(\overrightarrow{AC}\) sont orthogonaux.
\(\overrightarrow{AB}\) et \(\overrightarrow{AC}\) ne sont pas colinéaires donc le vecteur \(\overrightarrow{n}(1 ; - 2 ; 1)\) est normal au plan \((ABC)\).
Une équation du plan \((ABC)\) est donc de la forme \(x - 2 y + z + d = 0\).
$C$ appartient au plan \((ABC)\) donc \(6 - 2 \times 1 + 5 + d = 0\) et finalement : \(d = -9\).
Conclusion : Une équation du plan \((ABC)\) est : \(x -2 y + z - 9 = 0\).
Un vecteur est normal à un plan s’il est orthogonal à deux vecteurs non nuls et non colinéaires du plan.
Testez le produit scalaire.
Connaissant le vecteur normal, vous pouvez en déduire une partie de l’équation du plan.
Utilisez enfin le fait que \(C\) est par exemple un point du plan et concluez.
Question 4
Calculer la distance du point \(D\) au plan \((ABC)\). En déduire le volume $V$ du tétraèdre \(ABCD\).
D'après la formule démontrée en préambule,
\(d = \dfrac{|x_D-2y_D+z_D-9|}{\sqrt{1^2+(-2)^2+1^2}} \)
\(d= \dfrac{|4-2 \times 0 + (-1)-9|}{\sqrt{1^2+(-2)^2+1^2}} \)
\(d= \dfrac{6}{\sqrt{6}} = \sqrt{6}\)
Le volume du tétraèdre \(ABCD\) est égal à :
\(V=\dfrac{1}{3}A_{ABC} \times d \)
\(V= \dfrac{1}{3} \times \dfrac{9\sqrt{6}}{2} \times \sqrt{6} = 9\)u.v
La formule de la distance vous est donnée dans l’énoncé.
Un tétraèdre est une pyramide à base triangulaire. Vous connaissez l’aire de base (du triangle \(ABC\)) et la hauteur associée que vous venez de calculer.
Question 5
Partie C
Soit \(Q\) le plan d'équation \(x - 2 y + z - 5 = 0\).
1. Déterminer les positions relatives des deux plans \(Q\) et \((ABC)\).
Les plans \(Q\) et \((ABC)\) ont le même vecteur normal \(\overrightarrow{n}(1 ; - 2 ; 1)\) donc ils sont parallèles ou confondus.
On vérifie que le point $A$ n'appartient pas à $Q$ : \(3 - 2 \times (-2) + 2 - 5 =4 \neq 0\)
Les plans sont donc strictement parallèles.
Faites vous un brouillon et rappelez-vous des différentes positions relatives de deux plans.
Pour étudier cela, on s’intéresse aux vecteurs normaux.
Si deux vecteurs normaux de deux plans sont colinéaires alors les plans sont parallèles (ou confondus). Dans le cas contraires, ils seront sécants.
Question 6
\(Q\) coupe les droites \((DA)\), \((DB)\) et \((DC)\) respectivement en \(E\), \(F\) et \(G\).
Déterminer les coordonnées de \(E\) et montrer que \(E\) appartient au segment \([DA]\).
\(E\) appartient à \((DA)\) donc il existe un réel \(k\) tel que \(\overrightarrow{DE} = k\overrightarrow{DA}\).
Notons \(E\) le point de coordonnées \((x ; y; z)\).
On a : \(\left\{\begin{array}{left} x-4 = -k\\ y = -2k\\ z+1=3k\\ \end{array}\right.\Leftrightarrow \left\{\begin{array}{left} x=4-k\\ y=-2k\\ z=-1+3k\\ \end{array}\right.\)
De plus, \(E\in Q\) donc \((4 - k) - 2 \times (- 2 k) + (- 1 + 3 k) - 5 = 0\)
Soit : \(- 2 + 6 k = 0\)
Et finalement : \(k = \dfrac{1}{3}\).
En remplaçant \(k\) par \(\dfrac{1}{3}\), \(E\) a pour coordonnées \(\left( \dfrac{11}{3};-\dfrac{2}{3};0\right)\)
Ainsi : \(\overrightarrow{DE} = \dfrac{1}{3} \overrightarrow{DA}\)
Conclusion : \(E\) appartient au segment \([DA]\).
\(E \left(\begin{array}{left} x\\ y\\ z\\ \end{array}\right)\) appartient à la droite \((DA)\) donc le vecteur \(\overrightarrow{DE}\) est colinéaire au vecteur \(\overrightarrow{DA}\).
Le point \(E\) appartient aussi au plan \(Q\) donc ses coordonnées vérifient son équation. On trouve ainsi les coordonnées de \(E\).
Comparer les vecteurs \(\overrightarrow{DE}\) et \(\overrightarrow{DA}\). Prouvez ainsi que \(E\) appartient au segment \([DA]\).
Question 7
Dans cette question, toute trace de recherche,même incomplète, ou d'initiative,même non fructueuse, sera prise en compte dans l'évaluation.
Déterminer le volume $V'$ du tétraèdre \(EFGD\).
Le plan \(Q\) est aussi le plan \((EFG)\). Les plans \((EFG)\) et \((ABC)\) sont parallèles donc le tétraèdre \(EFGD\) se déduit du tétraèdre \(ABCD\) par une homothétie de centre \(D\) de rapport \(\dfrac{1}{3}\).
Le volume du tétraèdre \(EFGD\) est égal à :
\(V'=\dfrac{1}{3^3}V_{ABCD} \)
\(V'=\dfrac{1}{27}\times 9 \)
C’est une question un peu délicate. Faites une figure très soignée.
Pensez à une transformation du plan qui transformerait le Tétraèdre \(DABC\) en \(DEFG\).
Une homothétie bien sûr.
Son centre est bien sur \(D\). Son rapport est donné en disant que \(E\) est l’image de \(A\) par cette homothétie.
Concernant le volume, rappelez-vous que l’image d’un solide de Volume \(V\) par une homothétie de rapport \(k\) est un solide de volume \(k^3 \times V\).