L'énoncé
On note \(g\) la fonction définie sur \(\left[0; \dfrac{\pi}{2}\right]\) par : \(g(x) = 2x\cos (2x) - \sin(2x) + \dfrac{\pi}{2}\)
Question 1
La fonction \(g\) est-elle-\(\pi\)-périodique ?
\(g (x+\pi) = 2(x+\pi) \cos \left( 2(x+\pi)\right) - \sin \left( 2(x+\pi)\right) + \dfrac{\pi}{2} \)
\(g (x+\pi)= 2(x+\pi) \cos \left( 2x+2\pi\right) - \sin \left( 2x+2\pi\right) +\dfrac{\pi}{2} \)
\(g (x+\pi)= 2(x+\pi) \cos \left( 2x\right) - \sin \left( 2x\right) +\dfrac{\pi}{2} \)
On nobtient pas l'écriture de \(g(x)\) (car il y a le \(x+\pi\) au début de la formule, et il aurait fallu avoir \(x\) pour retomber exactement sur la formule de \(g(x)\)).
Donc \(g\) n'est pas \(\pi\)-périodique.
Écrire \(g (x+\pi)\).
On peut légèrement simplifier l’écriture en faisant apparaître par exemple \(\cos(x+2\pi)\).
Obtient-on la même formule que pour \(g(x)\) ?
Question 2
Montrer que \(g\) est dérivable sur \(\mathbb{R}\) et déterminer \(g'(x)\).
\(g\) est dérivable sur \(\mathbb{R}\) comme somme de fonctions dérivables sur \(\mathbb{R}\).
Posons \(h(x) = 2x\) \(\cos(2x)\) : c'est un produit !
\(u(x) = 2x\) et \(v(x) = \cos(2x)\)
\(u'(x) = 2x\) et \(v'(x) = -2\sin(2x)\)
Alors :
\(h'(x) = u'(x) \times v(x) + u(x)\times v'(x)\)
\(h'(x) = 2\cos(2x)+2x \times (-2\sin(2x))\)
\(h'(x) = 2\cos(2x) - 4x\sin(2x)\)
Comme \(g(x) = h(x) -\sin(2x) + \dfrac{\pi}{2}\)
On en déduit que :
\(g'(x) = h'(x) -2\cos(2x) \)
\(g'(x) = 2\cos(2x)-4x\sin(2x) - 2\cos(2x)\)
\(g'(x)= -4x\sin(2x)\)
Conclusion : on a \(g'(x) = -4x\sin(2x)\)
Commencez par dériver le début de l’écriture : on peut poser \(h(x) = 2x\) \(\cos(2x)\) trouve la dérivée de \(h\) ! Quelles formules de cours vont servir ici ?
Pour dériver \(cos(2x)\) on a la formule \( [\cos(ax+b)]'= -a\sin (ax + b)\), (voir vidéo sur la dérivation des fonctions trigonométriques) et bien sûr on a un produit \(2x\times \cos(2x)\) !
La dérivée de \(\cos(2x)\) est \(-2\sin(2x)\). À vous de terminer le calcul grâce à \((u + v)' = u'v + uv\) !
Question 3
Résoudre dans \(\mathbb{R}\) l'équation \(g'(x)=0\)
\(g'(x) = 0 \Leftrightarrow -4x \times \sin (2x) = 0\)
\(\Leftrightarrow \left\{\begin{array}{left} -4x =0\\ \sin (2x) = 0 \end{array}\right.\)
\(\Leftrightarrow \left\{\begin{array}{left} x = 0\\ 2x = 0 + 2k\pi\\ 2x =\pi +2k\pi \end{array}\right.\)
\(\Leftrightarrow \left\{\begin{array}{left} x = 0\\ x = k\pi\\ x = \dfrac{\pi}{2} + k\pi \end{array}\right.\)
Les solutions dans \(\mathbb{R}\) sont donc les réels \(x\) s'écrivant : \( x = k\pi\) ou \(x = \dfrac{\pi}{2}+ k\pi\) pour \(k \in \mathbb{Z}\).
Nous n'avons pas oublié la valeur \(x = 0\) : elle fait partie des valeurs proposées : il suffit de prendre \(k = 0\) dans la première formule \( x = k\pi\).
Déjà, il y a la règle de produit nul…
Pour résoudre \(\sin(2x) = 0\) , on utilise le cercle : pour quelles valeurs de \(X\) a-t-on \(\sin(X) = 0\) ?
\(\sin(X) = 0 \Leftrightarrow X =0 + 2k\pi\) ou \(X = \pi + 2k\pi\) et il suffit de mettre \(2x\) à la place de \(X\) ! Ensuite on isole \(x\), sans oublier de diviser les \(2k\pi\) par \(2\) !
Question 4
On se place maintenant sur \( \left[0;\dfrac{\pi}{2}\right]\), et on mène l'étude de \(g\) sur cet intervalle.
Donner les solutions de \(g'(x) = 0\) sur \( \left[0; \dfrac{\pi}{2}\right]\).
Les solutions de l'équation sont les réels \(x\) donnés par : \( x = k\pi\) ou \( x = \dfrac{\pi}{2} + k\pi\). $k\in \mathbb{Z}$
On cherche les valeurs qui sont dans \( \left[0; \dfrac{\pi}{2}\right]\) :
Il y a uniquement \( x = 0 \) ou \( x = \dfrac{\pi}{2}\).
Il faut juste chercher les valeurs qui sont dans \( \left[0; \dfrac{\pi}{2}\right]\) parmi les \( x = k\pi\) ou \( x = \dfrac{\pi}{2} + k\pi\).
Question 5
Étudier le signe $g$ sur l'intervalle \(\left[0; \dfrac{\pi}{2}\right]\).
On a \(g'(x) = -4x \sin(2x)\)
Le signe \(g'(x)\) dépend du signe de \(-4x\) et du signe de \(sin(2x)\) :
Et n'oublions pas que l'étude ne se fait que sur \( \left[0; \dfrac{\pi}{2}\right]\).
Sur\( \left[0; \dfrac{\pi}{2}\right]\) on a \(-4x \leq 0\)
Lorsque \(0 \leq x \leq \dfrac{\pi}{2}\) on a \( 0 \leq 2x \leq \pi\).
Or sur \([0; \pi]\) le sinus est positif (dessinez le cercle trigonométrique : si \( 0 \leq X \leq \pi\) alors on a \(\sin(X) \geq 0\)) : donc \(\sin(2x) \geq 0\).
Tableau de signes :

Étudiez séparément le signe de \(-4x\) et le signe de \(\sin(2x)\). Et attention uniquement sur \(\left [0; \dfrac{\pi}{2}\right]\).
\(2x\) varie entre \(0\) et \(\pi\) : quel est le signe du sinus sur \([0; \pi]\) ?
Rassemblez les informations obtenues dans le tableau de signes, en mettant bien les valeurs où la dérivée s’annule.
Question 6
En déduire le tableau de variations de \(g\) sur \( \left[0; \dfrac{\pi}{2}\right]\).
On obtient :
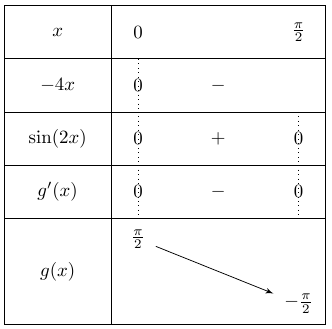
Détail du calcul des images :
\(g(0)= 0 - \sin(0) + \dfrac{\pi}{2} = \dfrac{\pi}{2}\)
\(g\left(\dfrac{\pi}{2}\right) = \pi \cos(\pi) - sin(\pi) + \dfrac{\pi}{2} = - \pi - 0 + \dfrac{\pi}{2} = - \dfrac{\pi}{2}\)
N’oubliez pas de compléter votre tableau avec les images de \(0\) et de \( \dfrac{\pi}{2}\).
Question 7
Montrer que l'équation \(g(x)=0\) possède une unique solution \(\alpha\) dans \( \left[0; \dfrac{\pi}{2}\right]\).
Hypothèse 1 : la fonction \(g\) est continue sur \( \left[0; \dfrac{\pi}{2}\right]\).
Hypothèse 2 : \(g\) est strictement croissante sur \( \left[0; \dfrac{\pi}{2}\right]\).
Hypothèse 3 : \(g(0) = \dfrac{\pi}{2} > 0\) et \( g\left(\dfrac{\pi}{2}\right) = -\dfrac{\pi}{2} < 0\),
De plus, \( 0 \in \left]-\dfrac{\pi}{2}; \dfrac{\pi}{2}\right[\).
Donc d'après une conséquence du théorème des valeurs intermédiaires l'équation \(g(x) = 0\) possède une unique solution \(\alpha\) dans\( \left[0; \dfrac{\pi}{2}\right]\)
Des connaissances de cours liées à la continuité sont utiles ici… Il y a 3 hypothèses à vérifier ! (Voir vidéo Théorème des valeurs intermédiaires en cas de doute.)
Une histoire de continuité, de stricte monotonie, sans oublier des valeurs de \(g(0)\) et de \(g \left(\dfrac{\pi}{2}\right)\).
Question 8
Préciser un encadrement de \(\alpha\) à \(10^{-2}\) près.
Grâce à la calculatrice on a :
\(g(0,95) \approx 0,0102\) et \(g(0,96) \approx -0,025\)
Donc \(0,95 < \alpha < 0,96\)
Fais un tableau de valeurs avec la calculatrice par exemple entre \(0\) et \(2\) avec un pas de \(0,2\) pour commencer et situer \( \alpha\).
On affine : faites le tableau entre \(0,8\) et \(1\) : quel pas faut-il choisir ?
On prend un pas de \(0,01\) pour obtenir la valeur de \(\alpha\) à \(10^{-2}\) près.
Question 9
Tracer la courbe dans un repère.
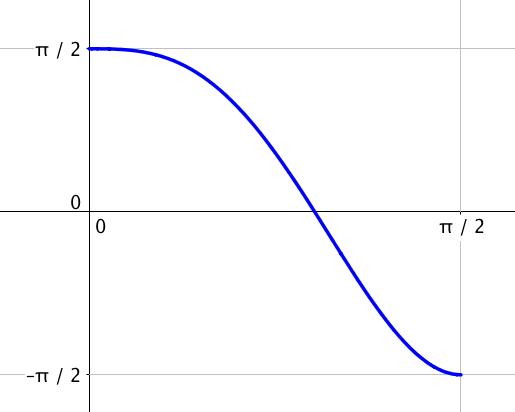
Pour information et en bonus, la voici sur un intervalle plus grand :
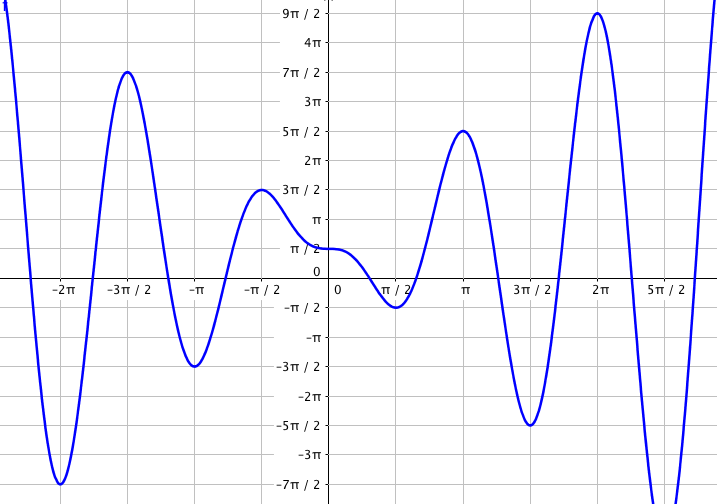
Choisissez bien les unités.
Utilisez les données du tableau de variations.
