L'énoncé
Répondez aux questions suivantes :
Question 1
Calculer la valeur de \(1+\cos(a)+\cos(2a)\) pour \(a = \frac{\pi}{3}\).
\(1+\cos(\frac{\pi}{3})+\cos(\frac{2\pi}{3}) = 1 + \frac{1}{2} + \cos(\pi - \frac{\pi}{3})\)
\(1+\cos(\frac{\pi}{3})+\cos(\frac{2\pi}{3}) =1+\frac{1}{2}-\frac{1}{2}\)
\(1+\cos(\frac{\pi}{3})+\cos(\frac{2\pi}{3}) =1\)
\(\cos(\frac{2\pi}{3}) = \cos(\pi-\frac{\pi}{3})\)
Pour calculer \(\cos(\pi-\frac{\pi}{3})\), utiliser que \(\cos(\pi-x)=-\cos(x)\)
Question 2
Calculer la valeur de \(1+\cos(a)+\cos(2a)\) pour \(a = -\frac{\pi}{6}\).
\(1+\cos(-\frac{\pi}{6}) + \cos(-\frac{2\pi}{6}) = 1+\frac{\sqrt{3}}{2}+\cos(-\frac{\pi}{3})\)
\(1+\cos(-\frac{\pi}{6}) + \cos(-\frac{2\pi}{6})=1+\frac{\sqrt{3}}{2}+\frac{1}{2}\)
\(1+\cos(-\frac{\pi}{6}) + \cos(-\frac{2\pi}{6})=\frac{3+\sqrt{3}}{2}\)
À quoi est égal \(\cos(-x)\) ?
On a \(\cos(-x) = \cos(x)\), et vous devez connaître les valeurs usuelles de cosinus.
Question 3
Montrer que : \(\cos(2a)=2\cos^2(a)-1\).
En déduire une factorisation de \(A =1+\cos(a)+\cos(2a) \)
On a : $\cos(2a)=\cos(a+a)$.
Or, $\cos(a+a)=\cos(a)\cos(a)-\sin(a)\sin(a)$
Ainsi, $\cos(2a)= \cos^2(a)-\sin^2(a)$
On utilise la relation fondamentale de la trigonométrie : $\cos^2(a)+\sin^2(a)=1$ ou encore $\sin^2(a)=1-\cos^2(a)$
$\cos(2a)= \cos^2(a)-(1-\cos^2(a))$
Et finalement : \(\cos(2a)=2\cos^2(a)-1\)
On a : \(A =1+\cos(a)+\cos(2a) \)
\(A= 1 + \cos(a)+2\cos^2(a)-1\)
\(A=\cos(a)+2\cos^2(a)\)
\(A=\cos(a)(1+2\cos(a))\)
Penser à : $\cos(2a)=\cos(a+a)$.
Puis utiliser ensuite la formule $\cos(a+b)=\cos(a)\cos(b)-\sin(a)\sin(b)$ en remplaçant $b$ par $a$.
On n'oubliera pas que $\cos^2(a)+\sin^2(a)=1$
Question 4
Résoudre dans \(\mathbb{R}\) l'équation trigonométrique \(1+\cos(a)+cos(2a)=0\)
Avec la forme factorisée, on peut résoudre :
\(1+\cos(a)+\cos(2a)=0\Leftrightarrow \cos(a)(1+2\cos(a))=0\)
\(\Leftrightarrow \left\{\begin{array}{left} \cos(a)=0\\ 1+2\cos(a) = 0 \end{array}\right.\)
\(\Leftrightarrow \left\{\begin{array}{left} \cos(a)=0\\ \cos(a) = -\frac{1}{2} \end{array}\right.\)
\(\Leftrightarrow \left\{\begin{array}{left} \cos(a)=\cos(\frac{\pi}{2})\\ \cos(a) = \cos(\frac{2\pi}{3}) \end{array}\right.\)
\(\Leftrightarrow a=\frac{\pi}{2}+2k\pi\) ou \(a=-\frac{\pi}{2}+2k\pi\) ou \(a=\frac{2\pi}{3}+2k\pi\) ou \(a=-\frac{2\pi}{3}+2k\pi\)
L’équation s’écrit : \(\cos(a)\times (1+2\cos(a))=0\)
On résout en appliquant d’abord la règle du produit nul : \(\cos(a)(1+2\cos(a))=0 \Leftrightarrow \cos(a)=0\) ou \(1+2\cos(a)=0\)
\(\Leftrightarrow \cos (a) = 0\) ou \(\cos(a)=-\frac{1}{2}\)
Résoudre alors chacune des deux équations à l’aide du cercle trigonométrique !
Question 5
En déduire dans l'intervalle \([0;2\pi]\), les solutions de l'équation :\(1+\cos(a)+\cos(2a)=0\)
On cherche ici les solutions qui appartiennent à l'intervalle \([0;2\pi]\).
On reprend les formules obtenues à la question 4 et on sélectionne les valeurs comprises entre 0 et \(2\pi\) :
\(a = \frac{\pi}{2}+2k\pi\) ou
\(a=-\frac{\pi}{2}+2k\pi\) ou
\(a=\frac{2\pi}{3}+2k\pi\) ou
\(a=-\frac{2\pi}{3}+2k\pi\)
Ainsi les solutions cherchées sont:
\(a = \frac{\pi}{2}\) (pour \(k=0\)),
\(a=\frac{3\pi}{2}\) (pour \(k=1\)),
\(a=\frac{2\pi}{3}\) (pour \(k=0\)),
\(a=\frac{4\pi}{3}\) (pour \(k=1\))
Vous devez ici choisir parmi les valeurs trouvées au 4 celles qui sont comprises entre $0$ et \(2\pi\).
Essayez les premières valeurs de \(k\) (soit \(k = 0, k =1\), ou peut-être \(k = -1\)).
Question 6
Résoudre dans \([0;2\pi]\) l'inéquation \(1+\cos(a)+\cos(2a) >0\)
On utilise : \(1+\cos(a)+\cos(2a)=\cos(a)(1+2\cos(a))\)
Il faut faire le tableau de signes de chaque facteur de l'inéquation : on a donc besoin du signe de \(\cos(a)\), et du signe de \(1+2\cos(a)\).
Tout cela s'obtient par des lectures faites sur le cercle trigonométrique : la technique est de faire décrire au nombre $a$ le cerle trigonométrique, en partant de $0$ jusquà \(2\pi\).
- Pour \(cos (a)\), c'est simple, on fait la lecture sur le cercle trigonométrique : \(\cos (a) \leq 0\Leftrightarrow a \in [0;\frac{\pi}{2}] \cup [\frac{3\pi}{2};2\pi]\)
- On a aussi : \(\cos(a) \geq 0\) pour \(a \in [\frac{\pi}{2};\frac{3\pi}{2}]\)
- Pour \(1+2\cos(a)\), on procède aussi par lecture graphique, et il faut commencer par remarquer que : \(2\cos(a)+1 \geq 0 \Leftrightarrow 2\cos(a) \geq -1 \Leftrightarrow \cos(a) \geq -\frac{1}{2}\)
- Puis on fait décrire au réel \(a\) tout le cercle trigonométrique, en partant de \(a = 0\) et en allant jusquà \(a = 2\pi\) et on situe le cosinus de \(a\) par rapport à \(-\frac{1}{2}\). On obtient les résultats suivants :
Pour \(a \in [0;\frac{2\pi}{3}]\), on a \(\cos(a) \geq - \frac{1}{2}\) et donc \(2\cos(a)+1 \geq 0\)
Pour \(a \in [\frac{2\pi}{3};\frac{4\pi}{3}]\), on a \(\cos(a) \leq - \frac{1}{2}\) et donc \(2\cos(a)+1 \leq 0\)
Pour \(a \in [\frac{4\pi}{3};2\pi]\), on a \(\cos(a) \geq - \frac{1}{2}\) et donc \(2\cos(a)+1 \geq 0\)
Ces informations sont ensuite à placer dans le tableau de signes :
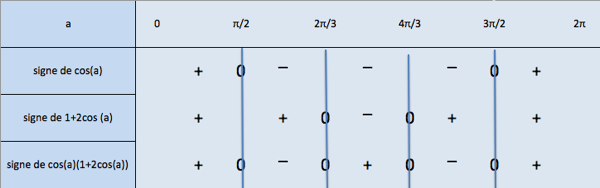
On lit l'ensemble solution de l'inéquation \(\cos(a)(2\cos(a)+1) >0\) :
\(S= [0;\frac{\pi}{2}[ \cup ]\frac{2\pi}{3};\frac{4\pi}{3}[ \cup ]\frac{3\pi}{2};2\pi]\)
Il faut ici s’aider de la factorisation obtenue au 3) : \(1+\cos(a)+\cos(2a)=\cos(a)(1+2\cos(a))\)
On a donc : \(1+\cos(a)+\cos(2a) > 0 \Leftrightarrow \cos(a)(1+2\cos(a)) > 0\).
On a besoin du signe de chaque facteur : \(\cos (a)\) et \(1+2\cos(a)\). Le tout par des lectures sur le cercle trigonométrique. Commence par établir le signe de \(\cos(a)\), c’est plus simple ! Attention n’oubliez pas que l’on demande la résolution sur l’intervalle \([0;2\pi]\) soit un tour complet du cercle en partant de $0$ et en allant jusqu’à \(2\pi\).
Pour le signe de \(1+2\cos(a)\), il faut remarquer que : \(2\cos(a)+1 \geq 2 \Leftrightarrow 2\cos(a)\geq -1 \Leftrightarrow \cos(a) \geq -\frac{1}{2}\)
On fait décrire à a la totalité du cercle, en partant de \(a = 0\) et en allant jusqu’à \(2\pi\). Lire alors les valeurs de \(a\) pour lesquelles \(\cos(a) \geq -\frac{1}{2}\). Constr
