Fiche de cours
Définition du logarithme népérien
Définition
La fonction logarithme népérien est l'unique fonction $f$, définie et dérivable sur $]0; +\infty[$ qui vérifie $\begin{array}{l} f(1) = 0 \\ f'(x) = \dfrac{1}{x} \end{array}$
On remarquera ici que l'on définit la fonction $f$ à partir de sa dérivée.
En outre, on peut noter que l'on ne connaissait jusqu'à présent pas de fonction dont la dérivée valait $\dfrac{1}{x}$.
En supposant que le cours portant sur les intégrales a déjà été étudié, on peut alors définir la fonction logarithme népérien, que l'on note $\ln$ comme étant la primitive de $x \mapsto \dfrac{1}{x}$ sur $]0; +\infty[$ et qui s'annule en $1$.
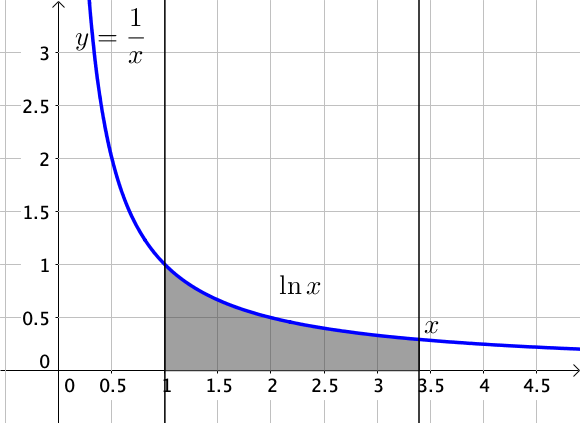
Ainsi, pour tout réel $x > 0$,
$\ln x = \displaystyle \int_1^x \dfrac{1}{t} dt$
On notera que lorsque $x = 1$, $\ln 1 = \displaystyle \int_1^1 \dfrac{1}{t} dt = 0$.
Graphiquement, la fonction $\ln x$ correspond à l'aire sous la courbe de la fonction inverse, comprise entre les droites verticales d'abscisse $1$ et $x$.