L'énoncé
Les habitants d’une ville sont frappés par une épidémie. Le nombre de malades en fonction du temps, exprimé en jour, est modélisé par la fonction \(f\) suivante sur \(D =[0 ; 30] \):
\( f(t) = - t^3 + 30 t^2\).
Le nombre dérivé \(f’(t)\) représente la vitesse de propagation de la maladie au jour \(t\).
Question 1
Étudier le sens de variation de \(f\).
\(f'(t) = - 3 t^2 + 60 t = t(-3t +60)\)
\(-3t+60>0 \Leftrightarrow t<20\)
\(t\) étant positif, \(f\) est croissante sur \([0 ; 20]\) et décroissante sur \([20 ; 30]\).
Il suffit de dériver \(f\).
Question 2
Calculer la dérivée seconde de \(f\). En déduire le sens de variation de \(f'\).
\(f''(t)=-6t+60\)
\(-6t+60>0\Leftrightarrow t<10\)
\(f'\) est donc croissante sur \([0 ; 10]\) et décroissante sur \([10 ; 30]\).
Il suffit de dériver \(f’\).
Question 3
La fonction \(f\) est-elle convexe ? Concave ? Interpréter ce résultat
\(f\) est convexe sur \([0 ; 10]\) et concave sur \([10 ; 30]\).
Lorsque la fonction est convexe, la vitesse de propagation est croissante, la maladie se répand donc plus vite.
Au bout de 10 jours, la fonction devient concave, cela correspond à un ralentissement de la vitesse de propagation de la maladie.
Regardez la vidéo sur les fonctions convexes et concaves.
Pour l’interprétation, utiliser la vitesse, c’est-à-dire \(f’(x)\). Lorsque \(f\) est convexe, \(f’\) est croissante. Une vitesse croissante correspond à une… accélération ! Faites de même lorsque \(f\) est concave.
Question 4
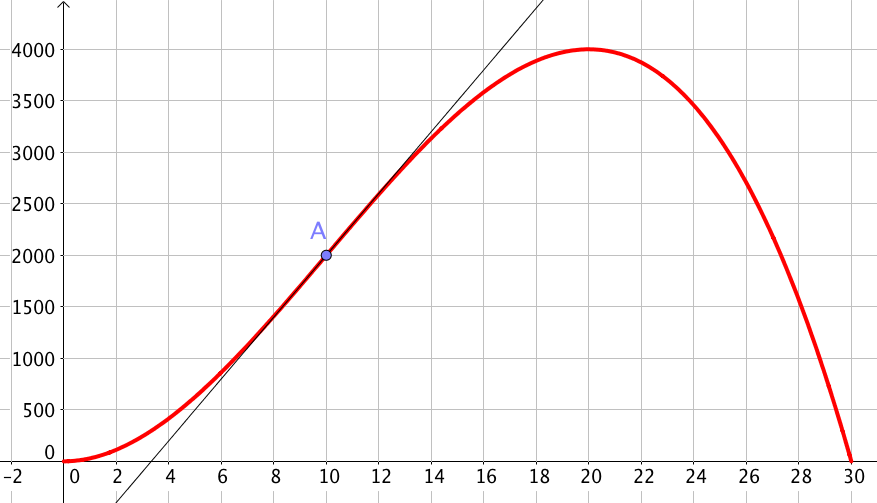
Démontrer que la courbe représentative de \(f\) admet un point d'inflexion. Que signifie-t-il ?
La courbe représentative de \(f\) admet un point d'inflexion si \(f''\) s'annule en changeant de signe.
\(f''(t)= 0 \Leftrightarrow -6t+60=0\Leftrightarrow t =10\)
D'après la question 2, \(f''\) change bien de signe en \(t=10\). Le point d'abscisse \(10\) est donc un point d'inflexion.
Concrètement, au dixième jour, l'accélération de la propagation devient négative, on voit donc un ralentissement de la vitesse de propagation de la maladie.
\(f\) admet un point d’inflexion lorsque… Un doute ? Regardez la vidéo dans les prérequis !
Pour l’interprétation, regardez le tableau de variation. Le point d’inflexion correspond au maximum de \(f’\). C’est donc le point pour lequel la fonction passe de convexe à concave. Qu’est-ce que cela signifie pour la vitesse de propagation ?
Question 5
Calculer la vitesse de propagation de la maladie le dixième jour.
\(f'(10) = -3\times10^2+600=-300+600=300\)
Au dixième jour, la vitesse de propagation est de 300 personnes par jour.
Il suffit de calculer \(f’(10)\) !
