Fiche de cours
Théorème des valeurs intermédiaires
Théorème
Soient $f$ une fonction continue sur un intervalle $I$ et $a$ et $b$ deux réels dans l'intervalle $I$ tels que $a\leqslant b $.
Alors, pour tout réel $k$ compris entre $f(a)$ et $f(b)$, il existe au moins un réel $c$ compris entre $a$ et $b$ tel que $f(c)=k$.
Illustration graphique
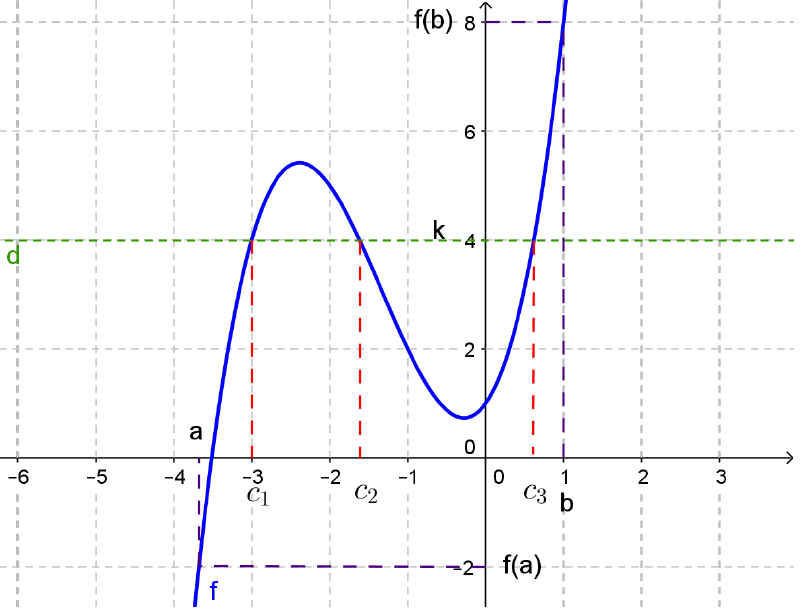
La fonction représentée en bleu est continue sur $I=[a,b]$.
Pour $k$ compris entre $f(a)$ et $f(b)$, on remarque graphiquement qu'il existe un $c_1$ dans $[a,b]$ tel que $f(c_1)=k$.
On voit, aussi qu'il existe deux autres $c_2$ et $c_3$ dans $[a,b]$ tels que $f(c_2)=k$ et $f(c_3)=k$. (D'où, dans le théorème, l'importance de l'expression "au moins")
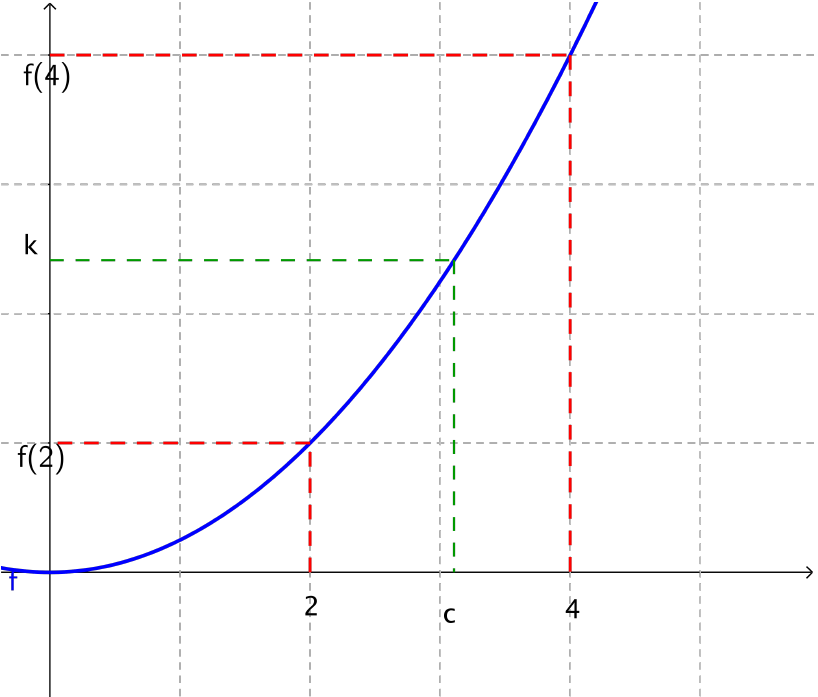
Cas des fonctions strictement monotones
Soit $f$ une fonction continue et strictement monotone sur un intervalle $[a,b]$ avec $a\leqslant b$.
Pour tout réel $k$ compris entre $f(a)$ et $f(b)$, il existe un unique réel $c$ compris entre $a$ et $b$ tel que $f(c)=k$.
Illustration graphique