L'énoncé
Les affirmations suivantes sont-elles exactes ? Justifier.
Question 1
La fonction \(f(x) = \dfrac{x-1}{x^2-1}\) définie sur \(]1, +\infty[\) est continue en $1$.
FAUX
La fonction n'est pas définie en $1$ donc elle ne peut pas être continue en ce point.
On note toutefois que \( f(x) = \dfrac{x-1}{x^2-1} = \dfrac{x-1}{(x+1)(x-1)} = \dfrac{1}{x+1}\)
Donc : \(\displaystyle\lim_{x \to 1^+}f(x) = \dfrac{1}{2}\)
Savez-vous démontrer qu’une fonction est continue en un point ? Si vous avez besoin d’un rappel, allez voir la vidéo associée dans les prérequis !
La fonction est-elle définie en $1$?
Si vous en avez la curiosité, cherchez pour la beauté du geste la limite de \(f\) lorsque \(x\) tend vers $1$ par valeurs supérieures.
\(x^2-1 = (x+1)(x-1)\) ! En simplifiant \(f,\) on peut calculer sa limite (à droite) en $1$.
Question 2
La fonction \(g\) définie sur \( \mathbb{R}\) par : \(\left\{ \begin{array}{left}g(x)= 0 \ \ si \ x=1 \ et \ x=-1 \\ g(x) =\dfrac{1}{x^2-1} \ \ \ \text{sinon} \end{array}\right. \) est continue en $1$.
FAUX
On a :
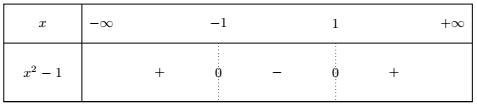
D'après ce tableau, \(\displaystyle\lim_{x \to 1^+} x^2-1 = 0^+ \)
Et en passant à l'inverse : \(\displaystyle\lim_{x \to 1^+} g(x) = +\infty \)
De même,
\(\displaystyle\lim_{x \to 1^-} g(x) = -\infty\)
La limite à gauche de $g$ en $1$ n'est pas égale à la limite à droite en $1$ donc $g$ n'admet pas de limite en $1$.
De plus, \(g(1) = 0\)
Donc par définition, \(g\) n'est pas continue en 1.
Savez-vous démontrer qu’une fonction est continue en un point ?
Il faut étudier les limites à droite et à gauche de $g$ en $1$
Cette limite existe t-elle ?
Est-elle égale à \(g(1)\) ? Qu’en conclue-t-on ?
Question 3
La fonction \(h\) définie sur \( \mathbb{R}\) par : \(\left\{ \begin{array}{left} h(x) =0 \ si \ x=1 \\ h(x) =x^2 + 2x -3 \ \text{sinon} \end{array}\right. \) est continue en $1$.
VRAI
\(\displaystyle\lim_{x \to 1} h(x) = 0 = h(1)\)
Savez-vous démontrer qu’une fonction est continue en un point ? Si vous avez besoin d’un rappel, allez voir la vidéo associée dans les prérequis !
Avez-vous calculé la limite de \(h\) en $1$ ? Que concluez-vous ?
Question 4
La fonction \(i\) définie sur \( \mathbb{R}\) par : \( i(x) = E(x-0,2)\) n'est pas continue en $1,2$.
VRAI
\(\displaystyle\lim_{x \to 1,2^-} i(x) = 0\)
or \(i(1,2)=1\) donc la fonction n'est pas continue en $1,2$
\(E\) est la fonction partie entière, que vaut \(i(1,2)\) ? N’hésitez pas à la représenter si vous avez un doute !
Quelle est la limite de \(i\) quand \(x\) tend vers $1,2$ par valeur inférieure ?
Question 5
La fonction \(j\) définie sur \( \mathbb{R}\) par : \(j(x) = |x| +2\) n'est pas continue en 0.
FAUX
La fonction valeur absolue est continue en zéro et :
\(\displaystyle\lim_{x \to 0} j(x) = 0 +2 = 2 = j(0)\)
La fonction \(j\) est donc continue en \(0\)
Savez-vous démontrer qu’une fonction est continue en un point ? Si vous avez besoin d’un rappel, allez voir la vidéo associée dans les prérequis !
Quelle est la limite de \(j\) en 0 ?
