L'énoncé
Cocher la ou les bonnes réponses
Tu as obtenu le score de
Question 1
Quel(s) énoncé(s) est/sont correct(s) ?
Pour tout réel $\delta >0$,
$\lim \limits_{n \to +\infty} P(|M_n - \mu| \geq \delta) = 0$
Pour tout réel $\delta >0$,
$\lim \limits_{n \to +\infty} P(|M_n - \mu| \geq \delta) = 1$
Pour tout réel $\delta >0$,
$\lim \limits_{n \to +\infty} P(M_n \in [\mu - \delta; \mu + \delta]) = 1$
C'est une bonne réponse !
On pourra revoir la vidéo au besoin.
Question 2
On considère un dé à 6 faces non truqué.
On note $X_i$ la variable aléatoire qui prend la valeur $1$ si le $6$ apparait au $i$-ème lancer.
On pose $M_n = \dfrac{X_1+...+X_N}{n}$
Que vaut $\lim \limits_{n \to +\infty} P(M_n \in \left [\dfrac{1}{6} - 0.005; \dfrac{1}{6} + 0.005 \right] $ ?
$0$
$1$
Chaque variable aléatoire $X_i$ suit une épreuve de Bernoulli, d'espérance $\dfrac{1}{6}$.
Par application de la loi faible des grands nombres avec $\delta = 0.05$, on trouve : $\lim \limits_{n \to +\infty} P(M_n \in \left [\dfrac{1}{6} - 0.005; \dfrac{1}{6} + 0.005\right] = 1$
$\dfrac{\pi}{4}$
On appliquera la loi en choisissant un $\delta$ particulier.
Question 3
Soit $(X_1, ... X_n)$ un échantillon de variable aléatoire d'espérance $200$.
On pose $M_n = \dfrac{X_1+...+X_n}{n}$
Que vaut $\lim \limits_{n \to +\infty} P(M_n \geq 220)$ ?
On ne peut pas savoir
$0$
En effet, $ P(M_n \geq 220) \leq P(|M_n-200| \geq 20) $
Or $\lim \limits_{n \to +\infty} P(|M_n-200| \geq 20) = 0$ d'après la loi faible des grands nombres.
En outre, $P(M_n \geq 220) \geq 0$
Ainsi, d'après le théorème des gendarmes, $\lim \limits_{n \to +\infty} P(M_n \geq 220) = 0$
$1$
On utilisera le fait que $P(M_n \geq 220) = P(M_n - 200 \geq 20)$
Question 4
Que vaut $\lim \limits_{n \to +\infty} P(M_n = \mu)$ ?
1
0
On ne peut pas savoir
En effet la loi faible des grands nombres est vraie pour tout réel strictement positif $\delta$. On ne peut donc pas l'appliquer pour $\delta = 0$
On se demandera si on peut appliquer l'inégalité pour $\delta = 0$
Question 5
On souhaite modéliser une variable aléatoire $X_i$ qui prend des valeurs entières entre 1 et 4, distribuées uniformément.
On considère la variable aléatoire $M_n = \dfrac{X_1+...+X_n}{n}$ que l'on simule 1000 fois à l'aide de l'algorithme suivant :
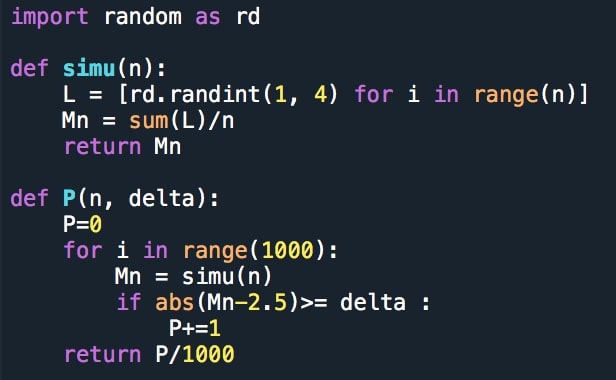
Que peut retourner $P(5000, 0.05)$ ?
$0.95$
$0.1$
$0.0018$
En effet, $\mathbb{E}(X_i) = \dfrac{1}{4}\times 1 + \dfrac{1}{4}\times 2 + \dfrac{1}{4}\times 3+ \dfrac{1}{4}\times 4 = 2.5$
En simulant 1000 fois la variable aléatoire $M_n$, on suppose que l'on obtient une bonne approximation de $P(|M_n - 2.5| \geq \delta)$.
Ici, on calcule $P(|M_{5000} - 2.5| \geq 0.05)$.
Or, $\lim \limits_{n \to +\infty} P(|M_{n} - 2.5| \geq 0.05) = 0$.
On choisit donc la valeur la plus petite car on peut considérer que $n = 5000$ est une bonne approximation de $n \to + \infty$.
On pourra commencer par calculer $\mathbb{E}(X_i) $

C'est effectivement un énoncé de la loi faible des grands nombres.