Partie A
On considère la fonction $h$ définie sur l’intervalle $[0; +\infty[$ par : $h(x) = xe^{-x}.$
1) Déterminer la limite de la fonction $h$ en $+\infty.$2) Étudier les variations de la fonction $h$ sur l’intervalle $0;+\infty$ et dresser son tableau de variations.
3) L’objectif de cette question est de déterminer une primitive de la fonction $h.$
a) Vérifier que pour tout nombre réel $x$ appartenant à l’intervalle $[0; +\infty[,$ on a :
$h(x) = e^{-x}-h'(x)$
où $h'$ désigne la fonction dérivée de $h.$
b) Déterminer une primitive sur l’intervalle $[0; +\infty[$ de la fonction $x \to e^{-x}.$
c) Déduire des deux questions précédentes une primitive de la fonction $h$ sur l’intervalle $[0;+\infty[$.
Partie B
On définit les fonctions $f$ et $g$ sur l’intervalle $[0; +\infty[$ par :
$f(x)= xe^{-x} + ln(x+1)$
et $g(x) =ln(x+1).$
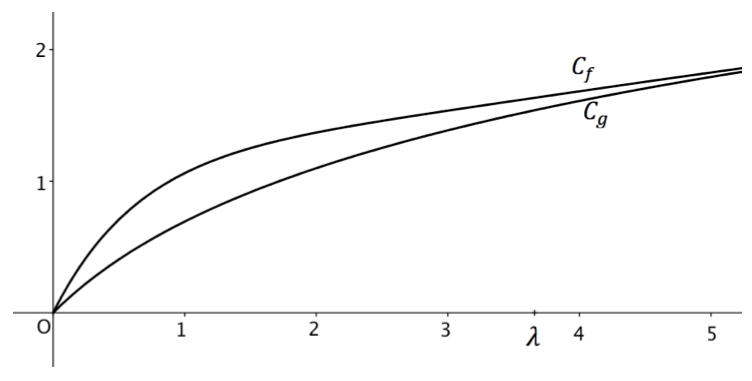
On note $C_f$ et $C_g$ les représentations graphiques respectives des fonctions $f$ et $g$ dans un repère orthonormé.
Ces deux courbes sont tracées en annexe.
1) Pour un nombre réel $x$ appartenant à l’intervalle $[0; +\infty[,$ on appelle $M$ le point de coordonnées $(x;f(x))$ et $N$ le point de coordonnées $(x;g(x)) : M$ et $N$ sont donc les points d’abscisse $x$ appartenant respectivement aux courbes $C_f$ et $C_g$.
a) Déterminer la valeur de $x$ pour laquelle la distance $MN$ est maximale et donner cette distance maximale.
b) Placer sur le graphique fourni en annexe les points $M$ et $N$ correspondant à la valeur maximale de $MN.$
2) Soit $\lambda$ un réel appartenant à l’intervalle $[0; +\infty[.$ On note $D_{\lambda}$ le domaine du plan délimité par les courbes $C_f$ et $C_g$ et par les droites d’équations $x = 0$ et $x = \lambda.$
a) Hachurer le domaine $D_{\lambda}$ correspondant à la valeur $\lambda$ proposée sur le graphique en annexe.
b) On note $A_{\lambda}$ l’aire du domaine $D_{\lambda},$ exprimée en unités d’aire. Démontrer que :
$A_{\lambda} = 1 - \frac{\lambda+1}{e^{\lambda}}$
c) Calculer la limite de $A_{\lambda}$ lorsque $\lambda$ tend vers $+\infty$ et interpréter le résultat.
3) On considère l’algorithme suivant :
Variables :
$\lambda$ est un réel positif
$S$ est un réel strictement compris entre 0 et 1.
Initialisation :
Saisir $S$
$\lambda$ prend la valeur 0
Traitement :
Tant que $1 - \frac{\lambda+1}{e^{\lambda}} < S$ faire
$\lambda$ prend la valeur $\lambda +1$
Fin tant que
Sortie :
Afficher $\lambda$
b) Quel est le rôle de cet algorithme ?
Annexe :