L'énoncé
Pour chacune des questions suivantes, choisis la (ou les) phrase(s) qui sont vraie(s).
Tu as obtenu le score de
Question 1
Le cercle \(\mathscr{C}\) a pour rayon 3 cm.
On peut dire que :
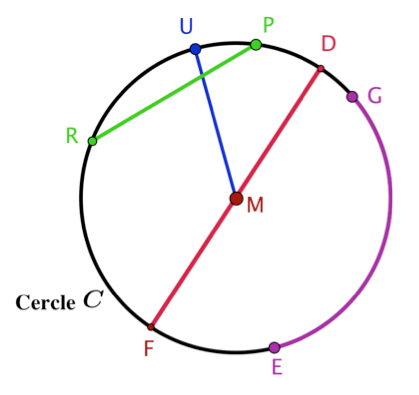
\(M\) est le centre du cercle \(\mathscr{C}\).
\(M\) est le milieu du cercle \( \mathscr{C}\).
\(M\) est le milieu de \([FD]\).
\(M\) est un point du cercle \( \mathscr{C}\).
Un cercle possède toujours un centre…
Et un segment possède un milieu ! Attention à ne pas confondre les deux termes…
Pour qu’un point soit sur le cercle, il doit bien être sur la ligne qui dessine ce cercle, et pas à l’intérieur…
\(M\) est le centre du cercle \(\mathscr{C}\), et aussi le milieu de \([FD]\). Propositions 1 et 3 vraies.
Attention, on ne peut pas utiliser le mot milieu pour parler du centre d’un cercle ! Proposition 2 fausse.
Enfin, \(U\) n’est pas sur le cercle. Proposition 4 fausse.
Le point \(M\) est à l’intérieur du disque délimité par le cercle \(\mathscr{C}\) : le mot « cercle » désigne le contour, et le mot « disque » en désigne l’intérieur.
Question 2
Le cercle \(\mathscr{C}\) a pour rayon 3 cm.
On peut dire que :
\([MU\)] est un rayon du cercle \(\mathscr{C}\).
\([DF\)] est le diamètre du cercle \(\mathscr{C}\).
\([DF\)] est un diamètre du cercle \(\mathscr{C}\).
\([DF\)] est un rayon du cercle \(\mathscr{C}\).
Connais-tu bien la différence entre rayon et diamètre ? Revois la figure de la fiche de révision ou la vidéo sur ce vocabulaire.
Un rayon relie le centre du cercle et un point du cercle, alors que un diamètre passe par le centre du cercle, mais relie deux points de ce cercle.
Fais attention à tous les mots employés : la proposition 2 n’est pas exactement la même que la 3 !
Un cercle possède plusieurs diamètres, et pas juste un seul…
Un rayon est un segment qui relie le centre du cercle à un point du cercle :
\([MU]\) est un rayon du cercle \(\mathscr{C}\). Proposition 1 vraie.
\([DF]\) n’est pas un rayon du cercle \(\mathscr{C}\), mais c’est un diamètre ! Proposition 4 fausse.
Il y a plein d’autres diamètres (même s’ils ne sont pas tracés), donc on ne peut pas employés les mots « le diamètre ». Proposition 3 vraie et 2 fausse.
Question 3
\([RP]\) est :
Un rayon du cercle.
Une corde du cercle.
Un arc du cercle.
Un diamètre du cercle.
Revois bien le vocabulaire sur le cercle : \([RP]\) est un segment qui relie juste deux points du cercle, cela s’appelle…
Lorsqu’un segment relie deux points du cercle, sans passer par le centre, c’est une corde du cercle !
Apprends bien le vocabulaire vu dans la fiche de révision ou la vidéo… Tu utiliseras ces termes tout au long de ta scolarité au collège !
Question 4
La portion du cercle comprise entre les points \(E\) et \(G\) (en violet sur la figure) s'appelle :
Une corde.
Un segment.
Un quart de cercle.
Un arc.
Sa forme devrait te mettre sur la voie.
La portion du cercle comprise entre les points \(E\) et \(G\) est un arc ! Proposition 2 juste.
Question 5
On peut affirmer que :
\(MF = MD\)
\(MF =MU\)
\(MU\) mesure 3 cm.
\(FD\) mesure 3 cm.
La notation \(MF\) désigne la longueur du segment \([MF]\) : c’est un rayon !
\([MD]\) est aussi un rayon.
Tous les rayons ont la même longueur…
Relis bien l’énoncé : le rayon est de 3 cm.
Comme \([MU], [MF], [MD] \) sont trois rayons, ils ont tous la même longueur ! On a donc :
\(MF = MD \) Proposition 1 vraie.
\(MF =MU \) Proposition 2 vraie.
Le rayon du cercle est 3 cm (donné dans l’énoncé) donc \(MU\) mesure 3 cm. Propositions 3 vraie et 4 fausse (\(FD\) mesure 6 cm : c’est un diamètre).