L'énoncé
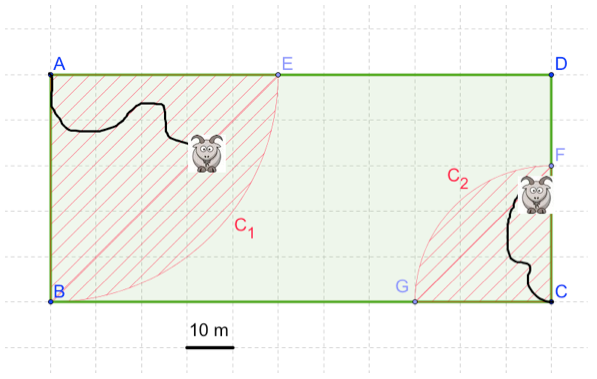
On considère un champ rectangulaire dans lequel deux chèvres sont attachées.
Les bêtes ont brouté toutes les zones hachurées en rouge en tendant au maximum la corde qui les retient.
On souhaite déterminer l’aire de la surface de pelouse restante.
Question 1
Calcule l'aire \(A_t\) du rectangle \(ABCD\).
\(A_t = L \times l\\ A_t = 110 \times 50\\ A_t = 5500 m^2\)
L'aire du terrain est de \(5500 m^2\).
C’est facile ! Il suffit de connaître la longueur et la largeur du rectangle.
Observe bien l’unité sur le graphique. Attention aux longueurs, ne te trompe pas.
\(A = L \times l\)
Question 2
Calcule l'aire \(A_1\) du quart de disque \(C_1\). (On prendra \(\pi\approx 3,14\))
Le quart de disque \(C_1\) a un rayon qui vaut \(50m\) daprès la figure On a donc :
\(A_1 = \large \frac{(\pi \times 50^2)}{4}\)
On divise par \(4\) car on calcule laire dun quart de disque.
\(A_1 \approx 1962,5 m^2\)
Un quart de disque est le quart d’un ? D’un disque bien sûr.
L’aire d’un disque vaut \(A = \pi \times r^2\)
Tu n’as qu’à calculer l’aire d’un grand disque imaginaire (qui serait toute la zone que peut atteindre une chèvre) et diviser par 4.
Question 3
Calcule finalement l'aire \(A_4\) de pelouse restante.
L'aire de la pelouse restante est bien sûr l'aire totale du champ à laquelle on a enlevé l'aire du champ brouté par les chèvres.
Ainsi :
\(A_4 = A_t-A_3\\ A_4 \approx 5\ 500-2\ 669\\ A_4 \approx 2\ 831 m^2\)
Tu avais l’aire totale du champ au début de l’exercice.
C’est \(A_t\).
Vas-tu maintenant enlever ou ajouter une aire ?
Question 4
Calcule l'aire \(A_2\) du quart de disque \(C_2\). (On prendra \(\pi\approx 3,14\))
Le quart de disque \(C_2\) a un rayon qui vaut \(30m\) d'après la figure.
On a donc :
\(A_2 = \large\frac{(\pi \times 30^2)}{4} \)
On divise par \(4\) car on calcule l'aire d'un quart de disque.
\(A_2 \approx 706,5 m^2\)
Un quart de disque est le quart d’un ? D’un disque bien sûr.
Tu n’as qu’à calculer l’aire d’un grand disque imaginaire (qui serait toute la zone que peut atteindre une chèvre) et diviser par 4.
L’aire d’un disque vaut \(A = \pi \times r^2\)
Question 5
Que vaut l'aire \(A_3\) totale broutée par les chèvres ?
\(A_3 = A_1+A_2\\ A_3 \approx 1962,5+706,5\\ A_3\approx 2\ 669 m^2\)
Facile, il suffit d’additionner ces deux aires !
