L'énoncé
Question 1
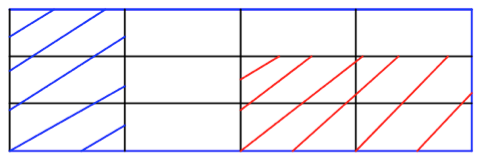
Quelle fraction non simplifiée de ce rectangle a-t-on hachurée en bleu ?
\(\dfrac{3}{12}\)
On a hachuré 3 parts en bleu parmi les 12 parts égales donc \(\dfrac{3}{12}\) de ce rectangle sont hachurées en bleu.
En combien de parties égales a-t-on partagé ce rectangle ?
Combien de parties a-t-on hachurées en bleu ?
Question 2
On peut donner une deuxième réponse à la première question. Laquelle et pourquoi ?
\(\dfrac{1}{4}\)
1 colonne parmi les 4 colonnes (4 parts égales) de ce rectangle est hachurée donc la fraction vaut \(\dfrac{ 1}{4}\).
Et aussi : \(\dfrac{3}{12} = \dfrac{3\times 1}{3\times 4} = \dfrac{1}{4}\)
Tu peux partager en colonnes. Combien y en a t-il?
Combien de colonnes sont hachurées en bleu ?
Tu peux simplifier ta réponse précédente pour répondre à celle-ci.
Question 3
Quelle fraction non simplifiée de ce rectangle a-t-on hachurée en rouge ?
\(\dfrac{4}{12}\)
4 parts hachurées en rouges parmi 12 parts égales donc la fraction vaut \(\dfrac{4}{12}\).
En combien de parties égales a-t-on partagé ce rectangle ?
Combien de parties a-t-on hachurées en rouge ?
Question 4
Quelle autre réponse peut-on donner à la question précédente ?
\(\dfrac{1}{3}\)
\(\dfrac{4}{12}=\dfrac{4\times 1}{4\times 3}=\dfrac{1}{3}\)
Simplifie la fraction, réponse précédente.
Tu peux déplacer les rectangles rouges pour les mettre en ligne.
1 ligne sur 3 est alors hachurée en rouge.
Question 5
Quelle fraction de ce rectangle n'est pas hachurée ?
\(\dfrac{5}{12}\)
5 parts parmi 12 parts égales ne sont pas hachurées donc \(\dfrac{5}{12}\) ne sont pas hachurées.
Autre raisonnement : parmi 12 parts égales, 3 sont hachurées en bleu et 4 en rouge.
Le reste est : \(12-(3+4)=12-7=5\).
Ainsi, 5 parmi 12 parts égales ne sont pas hachurées donc \(\dfrac{5}{12}\) du rectangle ne sont pas hachurés.
En combien de parties égales a-t-on partagé ce rectangle ?
Combien de parties n’a-t-on pas hachurées?