L'énoncé
Cet exercice est un QCM. Coche la bonne réponse.
Tu as obtenu le score de
Question 1
Quelle fraction de ce disque a-t-on hachurée en rouge ?
\(\dfrac{4}{3}\)
\(\dfrac{3}{4}\)
\(\dfrac{1}{3}\)
\(\dfrac{3}{8}\)
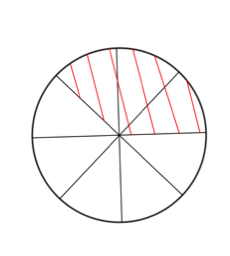
En combien de parts égales a-t-on partagé ce disque ?
Combien de ces parts égales sont hachurées ?
3 parts hachurées parmi 8 parts égales donc \(\dfrac{3}{8}\).
Question 2
Quelle fraction de ce rectangle a-t-on coloriée en rouge ?
\(\dfrac{3}{4}\)
\(\dfrac{4}{3}\)
\(\dfrac{3}{7}\)
\(\dfrac{7}{3}\)
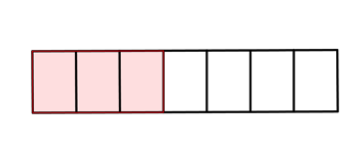
En combien de parts égales a-t-on partagé ce rectangle ?
Combien de ces parts égales sont hachurées ?
On a hachuré 3 parts parmi 7 parts égales donc \(\dfrac{3}{7}\).
Question 3
Écris \(\dfrac{3,8}{5}\) sous la forme d'une fraction.
\(\dfrac{7,6}{10}\)
\(3,8:5\)
\(\dfrac{38}{50}\)
\(\dfrac{38}{5}\)
Une fraction est une écriture fractionnaire dont le numérateur et le dénominateur sont des nombres entiers.
Tu dois multiplier le numérateur et le dénominateur par un même nombre
\(\dfrac{3,8}{5} = \dfrac{3,8\times 10}{5\times 10} = \dfrac{38}{50}\)
On aurait pu encore la simplifier :
\(\dfrac{38}{50} = \dfrac{19\times 2}{25\times 2} = \dfrac{19}{25}\)
Question 4
Écris \(\dfrac{6,37}{4,1}\) sous la forme dune fraction.
\(\dfrac{637}{410}\)
\(\dfrac{637}{41}\)
\(\dfrac{63,7}{41}\)
\(\dfrac{6370}{410}\)
Une fraction est une écriture fractionnaire dont le numérateur et le dénominateur sont des nombres entiers.
Tu dois multiplier le numérateur et le dénominateur par un même nombre.
\(\dfrac{6,37}{4,1}=\dfrac{6,37×100}{4,1×100}=\dfrac{637}{410} \)
Question 5
Simplifie la fraction \(\dfrac{35}{50}\).
\(\dfrac{3,5}{5}\)
\(\dfrac{350}{500}\)
\(\dfrac{7}{10}\)
\(\dfrac{7}{5}\)
Tu dois diviser numérateur et dénominateur par un même nombre.
35 et 50 sont divisibles par 5.
La réponse doit être une fraction.
\(\dfrac{35}{50}=\dfrac{7\times 5}{10\times 5}=\dfrac{7}{10}\)