L'énoncé
Cet exercice est un QCM. Une seule réponse est correcte.
Tu as obtenu le score de
Question 1
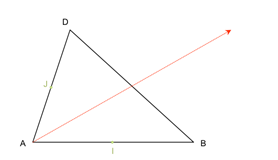
On considère un triangle quelconque \(ABD\). Soient \(I\) le milieu de \([AB]\) et \(J\) le milieu de \([AD]\).
On se place dans le repère \((A ; I ; J)\).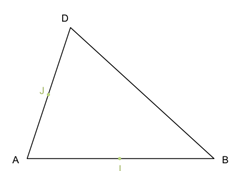
1. Quelles sont les coordonnées des points \(A\), \(B\) et \(D\) ?
\(A(0 ; 0) ; B(0 ; 2)\) et \(D(2 ; 0)\)
\(A(0 ; 0) ; B(2 ; 0)\) et \(D( 0 ; 2)\)
\(A(0 ; 0) ; B(0 ; 1)\) et \(D(1 ; 0)\)
Aucune des trois réponses précédentes n’est exacte.
Cas assez rare, le repère est ici quelconque. Oubliez vos habitudes de repère orthonormé le temps de cet exercice.
Dans le repère \((A ; I ; J)\), le vecteur unitaire de l’axe des abscisses est \(\overrightarrow{AI}\).
Ainsi \(I\) a pour coordonnées : \(I(1 ; 0)\).
Pour les mêmes raisons : \(J(0 ; 1)\).
Question 2
Calculez les coordonnées du vecteur \(\overrightarrow{AB} + \overrightarrow{AD}\).
\(\overrightarrow{AB}+\overrightarrow{AD}(-2 ; -2)\)
\(\overrightarrow{AB}+\overrightarrow{AD}(4 ; 4)\)
\(\overrightarrow{AB}+\overrightarrow{AD}(2 ; 2)\)
Aucune des trois réponses précédentes n’est exacte.
Savez-vous calculer les coordonnées d’une somme de vecteurs ? Allez voir la vidéo dans les prérequis.
Savez-vous construire la somme de deux vecteurs ? Allez voir la vidéo dans les prérequis.
Question 3
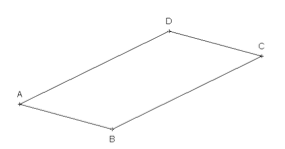
On souhaite construire un point \(C(x ; y)\) tel que \(ABCD\) soit un parallélogramme.
Ecrivez une égalité vectorielle qui caractérise le parallélogramme.
\(\overrightarrow{AB} =\overrightarrow{CD}\)
\(\overrightarrow{AB} =\overrightarrow{AD}\)
\(\overrightarrow{AB} =\overrightarrow{DC}\)
Aucune des trois réponses précédentes n’est exacte.
Savez-vous caractériser un parallélogramme avec deux vecteurs ?
Regardez cette figure : 
\(ABCD\) est un parallélogramme si et seulement si \(\overrightarrow{AB} = ...\) (par exemple).
Question 4
\(\overrightarrow{AB} =\overrightarrow{DC}\)
En déduire les coordonnées du point \(C(x ; y)\).
\(C(2 ; 2)\)
\(C(-2 ; 2)\)
\(C(2 ; -2)\)
Aucune des trois réponses précédentes n’est exacte.
Écrivez les coordonnées des deux vecteurs.
Résolvez ensuite l’équation résultant de \(\overrightarrow{AB} = \overrightarrow{DC}\).
Question 5
Quelle serait la nature du quadrilatère \(ABCD\) ainsi construit si le triangle \(ABD\) était rectangle en \(A\) ?
\(ABCD\) serait un losange.
\(ABCD\) serait un carré.
\(ABCD\) serait un rectangle.
Aucune des trois réponses précédentes n’est exacte.
Savez-vous ce qu’est un parallélogramme avec un angle droit ?
Besoin d’un rappel ? Allez voir la vidéo dans les prérequis.
Question 6
Quelle serait la nature du quadrilatère \(ABCD\) ainsi construit si le triangle \(ABD\) était rectangle isocèle en \(A\) ?
\(ABCD\) serait un losange.
\(ABCD\) serait un carré.
\(ABCD\) serait un rectangle.
Aucune des trois réponses précédentes n’est exacte.
Savez-vous ce qu’est un parallélogramme avec un angle droit et deux côtés consécutifs de même longueur ?
Besoin d’un rappel ? Allez voir la vidéo dans les prérequis.