Fiche de cours
La valeur absolue - Distance entre deux nombres
Définition : Valeur absolue
La valeur absolue d'un nombre $x$ se note $|x|$ et rend ce nombre positif.
Ainsi, si le nombre est positif, la valeur absolue du nombre est lui même.
Si le nombre est négatif, la valeur absolue est l'opposé de ce nombre.
On notera alors $\left \{ \begin{array}{l} |x| = x \text{ si } x \geq 0 \\ |x| = - x \text{ si } x \leq 0 \\ \end{array} \right.$
Exemples :
$|3| = 3$ car $3>0$
$|-2| = -(-2) = + 2$ car $-2 < 0$
$|\pi - 4 | = -(\pi - 4) = 4 - \pi$ car $\pi - 4 < 0$ en utilisant la calculatrice.
Distances
La distance entre deux nombres est toujours positive, on utilise donc la valeur absolue pour s'assurer de la positivité de nos calculs.
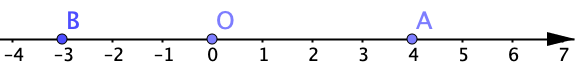
Exemples
On peut calculer des distances à l'origine.
Cette distance correspond à la valeur absolue de l'abscisse du nombre.
Ainsi, $|OA| = |4| = 4$ et $|OB| = |-3| = 3$.
