L'énoncé
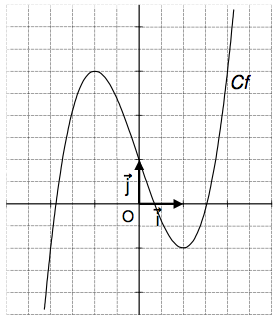
On a tracé dans le repère \((O;\overrightarrow{i};\overrightarrow{j})\) ci-contre, la courbe \(C_f\) représentative d’une fonction \(f\) définie sur \(\mathbb{R}\).
Question 1
Lire graphiquement les images par \(f\) de \(\dfrac{3}{2}, 0\) et \(-\dfrac{3}{2}\). .
Il semblerait que : \(f\left(\dfrac{3}{2}\right) = 0\) ; \(f(0) = 1\) et \(f\left(-\dfrac{3}{2}\right) = 2\).
Attention à la graduation !
Besoin d’un rappel sur l’image d’un nombre par une fonction ? Allez voir la vidéo dans les prérequis.
Question 2
Lire graphiquement le ou les antécédents de $-1$ par \(f\).
La fonction \(f\) admet deux antécédents de $-1$ : les nombres $-2$ et $1$.
Savez-vous ce qu’est un antécédent ? Allez voir la vidéo dans les prérequis.
Tracez une droite imaginaire, parallèle à l’axe des abscisses et passant par -1.
Question 3
Résoudre graphiquement l'équation \(f (x) = 1.\)
\(S = \{-1,75 ; 0 ; 1,75\}\)
Rechercher les antécédents de $1$ ou résoudre \(f(x) = 1\) revient au même.
Question 4
Résoudre graphiquement l'inéquation \(f (x) \geq 3\)
\(S = \{-1\} \cup [2 ; +\infty[\)
Il y a une valeur isolée dans la solution, il ne faut pas l’oublier.
Question 5
La courbe \(C_f\) représentée ci-contre est en fait celle de la fonction \(f\) définie sur \(\mathbb{R}\) par \(f (x) = x^3 - 3 x +1\).
Calculer les images par \(f\) de \(\dfrac{3}{2}, 0\) et \(-\dfrac{3}{2}\).
\(f\left(\dfrac{3}{2}\right) = \left(\dfrac{3}{2}\right)^3 - 3 \times \dfrac{3}{2} + 1\)
\(f\left(\dfrac{3}{2}\right)= \dfrac{27}{8} - \dfrac{9}{2} + 1\).
On réduit au même dénominateur :
\(f\left(\dfrac{3}{2}\right)= \dfrac{27-36+8}{8}\)
\(f\left(\dfrac{3}{2}\right) = - \dfrac{1}{8}\)
Ce n'est pas ce que nous avions imaginé en valeur approchée dans la première partie.
\(f(0) = 0^3-3\times 0+1=1\)
\(f(0)=1\)
\(f\left(-\dfrac{3}{2}\right) =\left(-\dfrac{3}{2}\right)^3 - 3 \times\left(-\dfrac{3}{2}\right) + 1\)
\( f\left(-\dfrac{3}{2}\right) = -\dfrac{27}{8}+\dfrac{9}{2} + 1\).
On réduit au même dénominateur :
\(f\left(-\dfrac{3}{2}\right)= \dfrac{-27 + 36 +8}{8}\)
\( f\left(-\dfrac{3}{2}\right) = \dfrac{17}{8}\).
Ce nombre ne vaut pas $2$. Là encore, elle diffère de la valeur approchée trouvée en question 1.
Question 6
\(f (x) = x^3 - 3 x +1\).
Résoudre par le calcul l'équation \(f (x) = 1\).
\(f(x) = 1\)
\( \Leftrightarrow x^3 -3x +1 = 1\)
\( \Leftrightarrow x^3-3x = 0\)
\( \Leftrightarrow x(x^2-3) = 0\) Ce produit de facteurs est nul si, et seulement si, l'un au moins des facteurs est nul.
\( \Leftrightarrow x = 0\) ou \( x^2 -3 = 0\)
\( \Leftrightarrow x = 0\) ou \(x^2 = 3\)
Cette deuxième équation du second degré admet deux solutions : \(\sqrt{3}\) et \(-\sqrt{3}\).
Besoin d'un rappel sur ces équations ? Voir la vidéo sur l'équation produit dans "Équations, inéquations"
Ainsi les solutions de l'équation sont : \(S = \{-\sqrt{3} ;0 ; \sqrt{3}\}\)
Avez-vous pensé à factoriser par \(x\) ?
Question 7
Tracez le tableau de variations de \(f\) sur \([-2 ; 2]\).
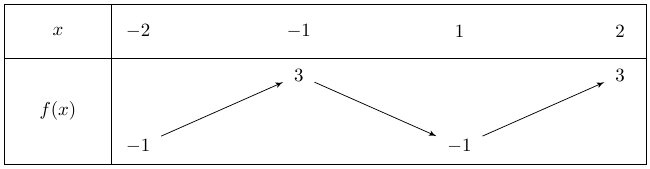
Besoin d’un rappel sur les tableaux de variations ? Attention à l’intervalle !
