Exercice – Résolution d’inéquations

 

Résoudre dans $\mathbb{R}$ les inéquations suivantes :

a) $  \dfrac{2}{3} x -5 \geq  \dfrac{4}{9}(x-5)$

On multiplie l’inégalité par $9$ :     $ \iff 6x-45 \geq 4(x-5)$.

On développe le terme de droite :  $ \iff 6x-45 \geq 4x-20$.

On regroupe les termes en $x$ :    $ \iff 6x-4x \geq  45 -20$.

On réduit :                          $ \iff 2x \geq  25$ 

Finalement :                                                  $ \iff  x \geq  \dfrac{25}{2}$  d’où :  $  S = \bigg[\dfrac{25}{2} ; +\infty \bigg[ $ .

 

 

b) $(x-2)(3x-1) > 3x-1$

le terme $(3x-1)$ est présent des deux cotés : $  \iff  (x-2)(3x-1) -3x-1 > 0$

on factorise par $ (3x-1) $ :                        $  \iff  (3x-1)[ (x-2) -1] > 0$

d’où :                                                             $  \iff  (3x-1) (x-3)  > 0$

les valeurs qui annulent les deux termes du produits sont : $\dfrac{1}{3}$ et $3$.

 

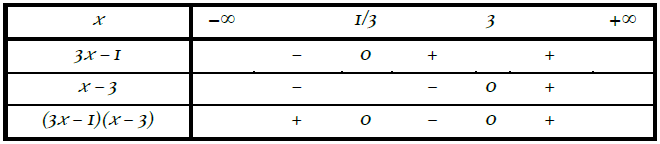
Donc:  $S = \bigg ] - \infty ; \dfrac{1}{3} \bigg[ \cup  \bigg] 3; +\infty \bigg[$

 

 c) $\dfrac{x^2 – x +2}{x+1} \leq 1$

remarque : la fraction n’est pas définie pour $x=-1$.

On passe le « 1 » à gauche et on réduit au même dénominateur :  $ \iff \dfrac{x^2 – x +2}{x+1} - \dfrac{ x +1}{x+1} \leq 0$.

On réduit le numérateur :     $ \iff \dfrac{x^2 – x +2}{x+1} - \dfrac{ x +1}{x+1} \leq 0$.

On « reconnait » l’identité remarquable :            $ \iff \dfrac{(x-1)^2 }{x+1}  \leq 0$.

Le numérateur est toujours positif, le signe du quotient est donc celui du dénominateur !

Donc $ S= ] - \infty ; -1[ $   ($-1$  est exclu à cause de la remarque  ci-dessus).