Fiche de cours
Vecteur directeur d'une droite, équation cartésienne
I) Définition
Soit $(\mathcal{D})$ une droite du plan,
on appelle vecteur directeur de $(\mathcal{D})$ tout vecteur non nul $\overrightarrow{u}$ qui possède la même direction que la droite $(\mathcal{D})$.
Si l'on connait deux points $A$ et $B$ de la droite, alors le vecteur $\overrightarrow{AB}$ est un vecteur directeur de cette dernière.
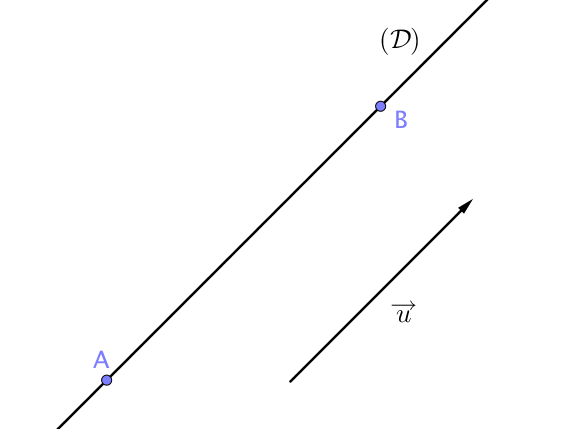
Comme le choix de $A$ et $B$ appartenants à le droite est arbitraire, il existe une infinité de vecteurs directeurs.
Tous ces vecteurs directeurs ont la même direction, celle de $(\mathcal{D})$, ils sont donc colinéaires.
Exemple :
On se place dans un repère.
On appelle $(\mathcal{d})$ la droite passant par les points $A(2;1)$ et $B(1;3)$. On souhaite donner les coordonnées d'un vecteur directeur de la droite $(\mathcal{d})$.
D'après la propriété précédente, on sait que le vecteur $\overrightarrow{AB}$ est un vecteur directeur de la droite, il ne reste donc
