L'énoncé
Une seule bonne réponse par question.
Tu as obtenu le score de
Question 1
Cochez la bonne réponse. Ceci est-il un patron d'un solide connu ?
Oui, d’un cône.
Oui, d’un cylindre.
Oui, d’une sphère.
Aucune des réponses précédentes n’est exacte.
Ne vous fiez pas à certaines dimensions très petites ou grandes.
Essayez mentalement de « fermer » ce patron.
Sinon, découpez une figure semblable et essayez de construire un solide.
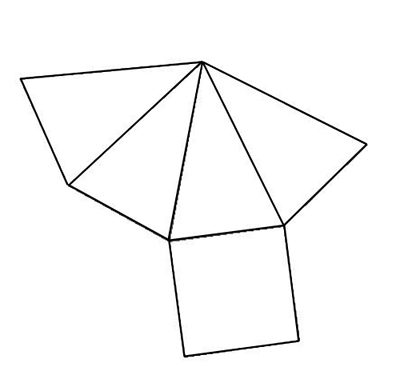
Question 2
De quel solide est-ce le patron ?
Un tétraèdre.
Une pyramide à base carrée.
Un prisme droit.
Aucune des réponses précédentes n’est exacte.
Vous pouvez aussi essayer de faire mentalement le même travail.
Si vous avez un doute, construisez le patron, découpez-le et essayez de former un solide.
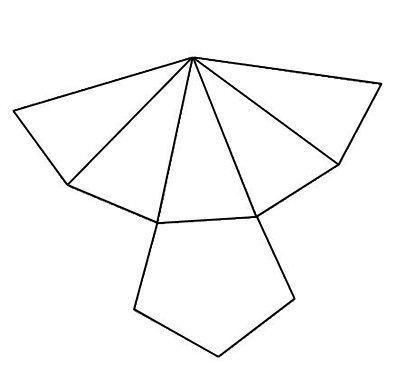
Question 3
De quel solide est-ce le patron ?
Un tétraèdre.
Une pyramide à base hexagonale.
Un prisme droit à base pentagonale.
Aucune des réponses précédentes n’est exacte.
Savez-vous comment se nomme un polygone à 5 côtés ?
Pensez au bâtiment qui abrite le département de la défense américaine.
Il s'agit du patron d’une pyramide régulière à base pentagonale.
Question 4
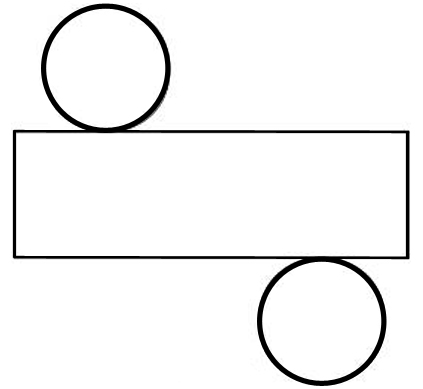
Ceci est le patron d'un cylindre de hauteur 5 cm et dont le rayon du disque de base mesure 2 cm. Quelles sont les dimensions exactes de la face latérale (le rectangle en somme) ?
\(5 cm \times 4 \pi cm\)
\(5 cm \times 8 \pi cm\)
\(5 cm \times 2 \pi cm\)
Aucune des réponses précédentes n’est exacte.
Une des deux dimensions est donnée : la hauteur.
Comparez l’autre dimension avec le périmètre du disque. Allez voir la vidéo dans les prérequis.
Question 5
On rappelle que le cylindre a pour hauteur 5 cm et le rayon du disque de base mesure 2 cm. Sachant que l'aire latérale vaut \(5 \ cm \times 4 \pi \ cm\), calculez alors l'aire totale \(A\) du cylindre. (Valeur exacte)
\(A = 22 \pi cm^2\)
\(A = 24 \pi cm^2\)
\(A = 28 \pi cm^2\)
Aucune des réponses précédentes n’est exacte.
Vous souvenez-vous de l’aire du disque ? Utilisez le formulaire de rappel donné au début du QCM.
Il y a trois faces. Deux disques et un rectangle.
Question 6
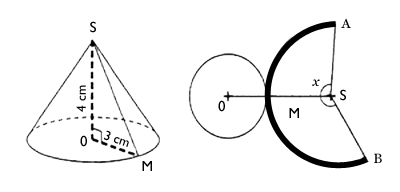
Voici un cône et son patron. On veut déterminer l'angle \(x\).
Dans un premier temps, calculez \(SM\).
\(SM = \sqrt{5} cm\)
\(SM = 25 cm\)
\(SM = 5 cm\)
Aucune des réponses précédentes n’est exacte.
Dans la représentation en perspective du cône, on remarque un triangle rectangle.
On pense donc immédiatement au célèbre théorème de…
Pythagore bien sûr.
Question 7
Dans la représentation du patron, que dire du grand arc de cercle \(AB\) (passant par \(M\)) et du périmètre du disque de base ?
On ne sait pas.
Ils sont égaux.
Ils sont différents.
Aucune des réponses précédentes n’est exacte.
Essayez mentalement de former la figure.
Sinon, découpez la figure et faites coïncider ces deux longueurs.
Question 8
Déterminez en fonction de \(x\) la longueur \(L\) de l'arc \(AB\).
\(L = 2 \times 5 \times \pi \times \dfrac{x}{360}\)
\(L = 5 \times \pi \times \dfrac{x}{360}\)
\(L = 2 \times 5 \times \pi \times \dfrac{2x}{360}\)
Aucune des réponses précédentes n’est exacte.
Un arc de cercle est une portion d’un cercle.
On sait que le rayon de l’arc vaut \(SM = 5\) cm.
Pour un angle \(x\) de 360°, le périmètre est celui d’un cercle.
Question 9
Finalement, pour que les longueurs soient égales, il faut que \(\frac{\pi\times x}{36}=6 \pi\).
Que vaut l'angle \(x\) ?
\(x = 210°\)
\(x = 216°\)
\(x = \frac{1}{6}°\)
Aucune des réponses précédentes n’est exacte.
Fais un produit en croix et simplifie par \(\pi\).
Question 10
Si le rayon de la base du cône double, la valeur de \(x\) double-t-elle ?
Non.
Oui.
Il faut refaire tous les calculs pour répondre.
Aucune des réponses précédentes n’est exacte.
Pour vous fixer les idées, multipliez 216° par deux…