L'énoncé
Question 1
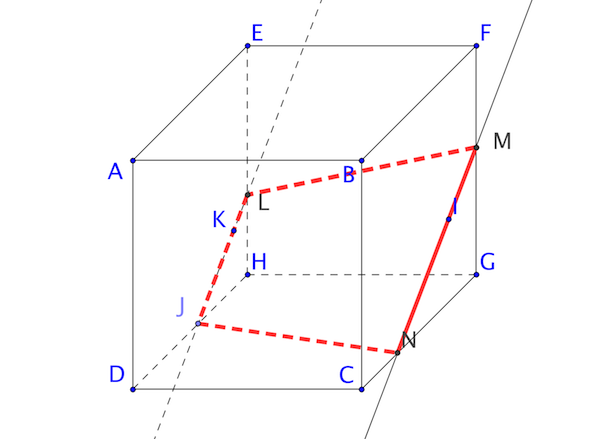
On considère le tétraèdre \(SABC\).
Les points \(I\), \(J\) et \(K\) sont respectivement des points de \((BCD)\), \([AD]\) et \((ABD)\).
Tracez en couleur la section du solide par le plan \((IJK)\).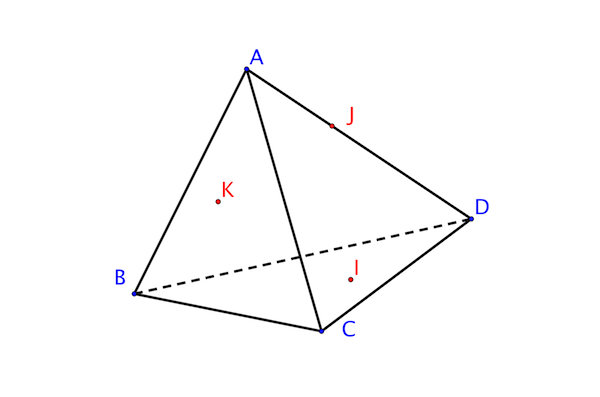 
Cherchez un point commun entre \((JK)\) et le plan \((BCD)\).
Pour cela, cherchez l’intersection de \((BD)\) et \((JK)\).
Question 2
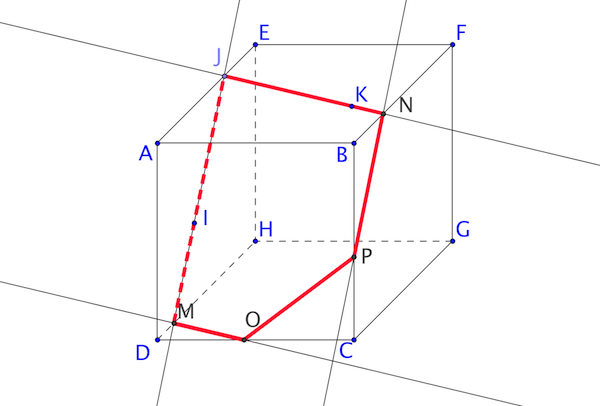
On considère le cube \(ABCDEFGH\).
Les points \(I\), \(J\) et \(K\) à sont respectivement des points de \([EH]\), \([EF]\) et \([GC]\).
Tracez en couleur la section du solide par le plan \((IJK)\).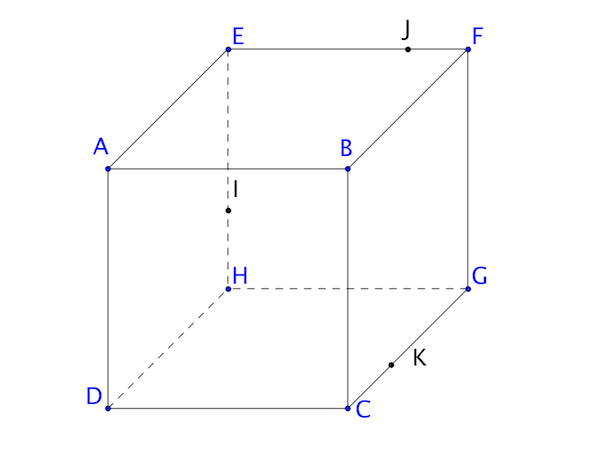
\([IJ]\) bien sûr.
Construisez l’intersection de \((IJ)\) et \((GH)\).
Ce point \(L\) appartient à la face \(BCGH\) donc vous pouvez tracer \((LK)\).
Question 3
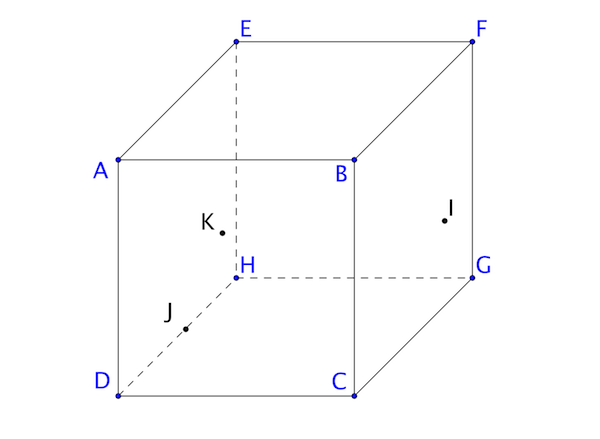
On considère le cube \(ABCDEFGH\). \(J\) est un point de \([AE]\).
Les points \(I\) et \(K\) sont respectivement des points de faces \(ADHE\) et \(ABFE\).
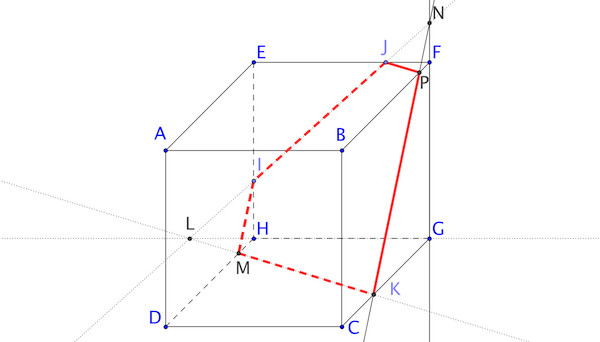
Tracez en couleur la section du solide par le plan \((IJK)\).
\((IJ)\) coupe \([DH]\) en \(M\) et \((JK)\) coupe \([BF]\) en \(N\).
Connaissez-vous cette propriété ? Si un plan coupe deux plans parallèles alors les intersections de ces plans forment deux droites parallèles.
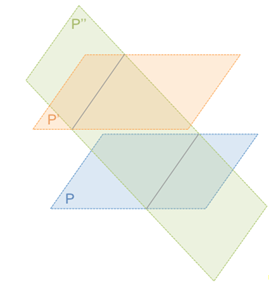
C’est la figure de la propriété précédente.
\(ABFE\) et \(DCGH\) sont parallèles donc tracez la parallèle à \((JN)\) passant par \(M\).
Question 4
On considère le cube \(ABCDEFGH\).
Les points \(I\) et \(K\) sont respectivement des points des faces \(BCGF\) et \(AEHD\).
Le point \(J\) appartient à \([DH]\).
Tracez en couleur la section du solide par le plan \((IJK)\).
Comment sont les faces \(AEHG\) et \(BFGC\) ?
Parallèles bien sûr. Vous pouvez donc utiliser le théorème vu dans la construction précédente.