L'énoncé
Une seule réponse est exacte.
Tu as obtenu le score de
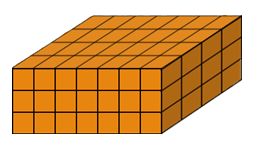
Question 1
Sachant que chaque petit pavé a pour dimensions \(1 \times 1 \times 2\) (unité : le m), calculez le volume du solide proposé.
84 m\(^3\)
168 m\(^3\)
840 m\(^3\)
Aucune des réponses précédentes n’est exacte.
Calculez le volume de chaque petit pavé
Combien y a t-il de petits pavés ?
Question 2
Quelle est alors l'aire totale \(A\) de ce solide ?
\(A = 100m^2\)
\(A = 101m^2\)
\(A = 102m^2\)
Aucune des réponses précédentes n’est exacte.
Les faces vont par paires. Il y en a six…
N’oubliez pas les dimensions des petits pavés : \(1 \times 1 \times 2\) m
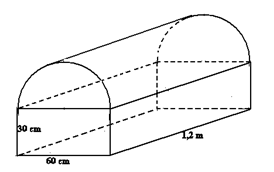
Question 3
On souhaite à présent calculer le volume du solide suivant :
Calculons dans un premier temps le volume du pavé. Soit \(V_1\) ce volume.
\(V_1 = 0,216 m^3\)
\(V_1 = 216 m^3\)
\(V_1 = 216 000 m^3\)
Aucune des réponses précédentes n’est exacte.
Attention aux unités.
Convertissez tout en mètres par exemple.
Question 4
Calculez à présent le volume \(V_2\) du demi-cylindre (valeur exacte). \(V_2\) est égale à :
\(V_2 = 0,027 \pi m^3\)
\(V_2 = 0,054 \pi m^3\)
\(V_2 = 54 000 \pi m^3\)
Aucune des réponses précédentes n’est exacte.
Connaissez-vous bien la formule du volume d’un cylindre ?
Il s’agit ici d’un demi-cylindre.
Attention à convertir dans les mêmes unités.
Question 5
\(V_1 = 0,216 m^3\)
\(V_2 = 0,054 \pi m^3\)
Déterminez à présent une valeur approchée au centième près par excès du volume total du solide.
\(0, 38 m^3\)
\(0, 385 m^3\)
\(0, 39 m^3\)
Aucune des réponses précédentes n’est exacte.
C’est la somme des deux volumes.
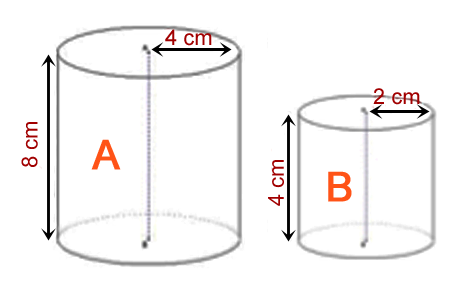
Question 6
Comparez l'aire totale de \(A\) et celle de \(B\).
L’aire de \(A\) vaut le double de celle de \(B\).
L’aire de \(A\) vaut la moitié de celle de \(B\).
L’aire de \(A\) vaut le quadruple de celle de \(B\).
Aucune des réponses précédentes n’est exacte.
Si chaque dimension d’un solide est doublée alors son aire est…?
Revoyez la vidéo dans les prérequis.
Question 7
Comparons à présent les volumes des cylindres \(A\) et \(B\).
Le volume de \(A\) vaut 8 fois celui de \(B\).
Le volume de \(A\) vaut 4 fois celui de \(B\).
Le volume de \(A\) vaut 2 fois celui de \(B\).
Aucune des réponses précédentes n’est exacte.
Si on double les dimensions d’un solide, son volume est multiplié par ?
\(2^3\)
Question 8
On considère une sphère incluse dans un cylindre. La sphère est tangente aux parois du cylindre.
Sachant que la sphère à un diamètre de 3m, calculez les dimensions du cylindre. On notera \(R\) le rayon de sa base et \(H\) sa hauteur.
\(R = 1,5m\) et \(H = 3m\)
\(R = 1,5m\) et \(H = 6m\)
\(R = 3m\) et \(H = 6m\)
Aucune des réponses précédentes n’est exacte.
Faites un brouillon si besoin.
Comparez la hauteur du cylindre et un diamètre de la sphère.
Question 9
Calculez à présent une valeur exacte du volume du cylindre.
\(V=13,5 \pi m^3\)
\(V=6,75 \pi m^3\)
\(V=27 \pi m^3\)
Aucune des réponses précédentes n’est exacte.
Il suffit d’appliquer la formule du cours.
Attention, on veut la valeur exacte.
Vous pouvez donc poser votre calculatrice.
Question 10
\(R = 1,5m\)
On note pour finir \(A_S\) et \(V_S\) les aires et volumes de la sphère. Donnez les deux valeurs exactes de ces grandeurs.
\(A_S= 9 \pi m^2\) et \(V_S=4,5 \pi m^3\)
\(A_S= 4,5 \pi m^2\) et \(V_S=4,5 \pi m^3\)
\(A_S= 9 \pi m^2\) et \(V_S=18 \pi m^3\)
Aucune des réponses précédentes n’est exacte.
C’est du cours. Connaissez-vous bien les formules ? Allez voir la vidéo dans les prérequis.
Le rayon \(R\) vaut ici 1,5m.