L'énoncé
Cocher la bonne réponse.
Tu as obtenu le score de
Question 1
La particularité des côtés d'un parallélogramme est...
Que tous ses côtés sont parallèles.
Qu'ils n'ont pas la même longueur.
Que ses côtés opposés sont égaux et parallèles deux à deux.
Un parallélogramme a ses côtés égaux deux à deux (opposés) et parallèles deux à deux également.
Il est impossible qu'un quadrilatère ait ses quatre côtés parallèles, cette réponse est donc à éliminer.
Enfin, un quadrilatère dont aucun des côtés n'a la même longueur est un quadrilatère quelconque, et non un parallélogramme.
Question 2
La particularité des diagonales d'un parallélogramme est...
Qu'elles se coupent en leur milieu et forment un angle droit à leur intersection.
Qu'elles se coupent en leur milieu.
Qu'elles forment un angle droit à leur intersection.
Les diagonales d'un parallélogramme se coupent en leur milieu mais ne forment pas d'angle droit comme dans un rectangle.
Question 3
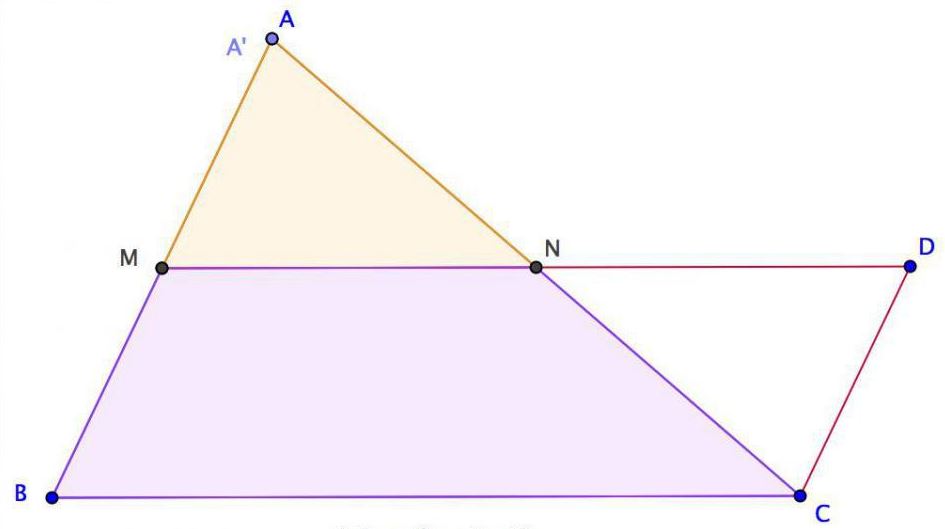
N est le milieu de [AC] et aussi celui de [MD].
M est le milieu de [AB]
Combien de parallélogrammes peut-on tracer avec ces points ?
(On peut tracer des segments supplémentaires si besoin).
$0$
$1$
$2$
$ADCM$ est un parallémogramme car ses diagonales ont le même milieu.
Ce n'est pas parce que $ADCM$ n'est pas tracé que ce n'est pas un parallélogramme...
$MB=DC$ et les segments sont parallèles donc $BMDC$ est aussi un parallélogramme
Question 4
Ce quadrilatère est-il un parallélogramme ?
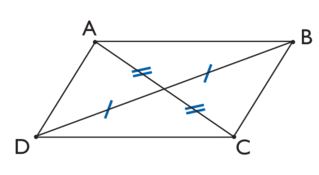
Oui
Non
Les diagonales ont le même milieu.
Question 5
Ce quadrilatère est-il un parallélogramme ?
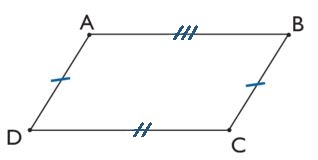
Oui
Non
$AB$ et $CD$ n'ont pas la même longueur (le codage de la figure le montre), attention à ne pas tomber dans le piège !
