Calculer le volume de ces trois solides, sachant que le solide jaune est un quart de sphère (arrondir les calculs au dixième près, on utilisera $\pi = 3,14$).
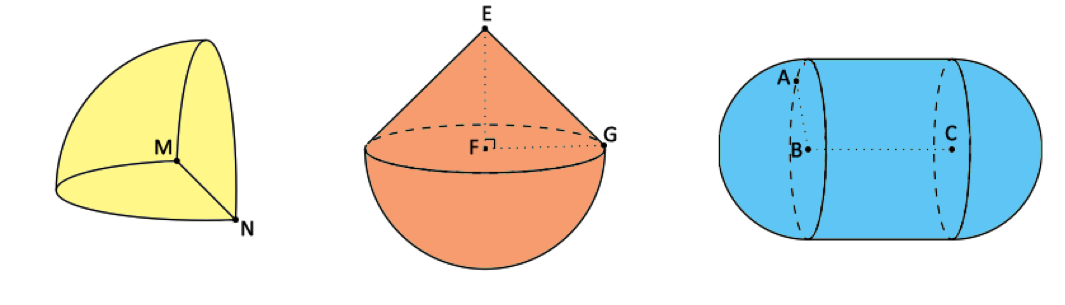
$MN = 16$ cm
$EF = FG = 4$ cm
$BC = 12$ cm et $AB = 6$ cm
1) Soit $V_1$ le volume du solide jaune
Ce solide est un quart de sphère de rayon $R = 8$ cm.
$V_1= (\dfrac{4}{3} \times \pi \times 8^3 ) \div 4$
$V_1= (\dfrac{4}{3} \times \pi \times 512) \div 4$
$V_1= (4,18 \times 512) \div 4$
$V_1= 2140,16 \div 4$
$V_1= 535,9$ cm$^3$
2) Soit $V_2$ le volume du solide orange :
$V_{cône}= \dfrac{\pi \times 4^2 \times 4}{3}$
$V_{cône}= \dfrac{200,96}{3}$
$V_{cône}= 67$ cm$^3$
$V_{demi-sphère}= (\dfrac{4}{3} \times \pi \times 4^3) \div 2$
$V_{demi-sphère}= (4,18 \times 64) \div 2$
$V_{demi-sphère}= 267,52 \div 2$
$V_{demi-sphère}=134$ cm$^3$
$V_2= 67 + 134$
$V_2= 201$ cm$^3$
3) Soit $V_3$ le volume du solide bleu :
Ce solide est composé de deux demi-sphères (de volume équivalent à une sphère) et d'un cylindre.
$V_{sphère}= (\dfrac{4}{3} \times \pi \times 6^3)$
