L'énoncé
Cet exercice est un QCM. Cochez la bonne réponse.
Tu as obtenu le score de
Question 1
Gabriel achète une glace à la vanille. Elle a la forme dune boule posée sur un cône comme sur la figure ci-dessous. Et il se demande s'il n'aurait pas intérêt à remplir le cône de glace à ras bord,plutôt que de poser la glace sur le cône vide.
De quelle(s) formules va-t-il avoir besoin pour trancher ce délicat problème de gourmandise ?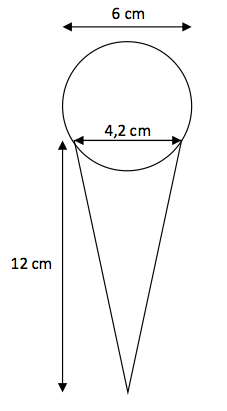
Formule du volume d’une boule.
Formule du volume d’un cône.
Formule du volume d’une boule et formule du volume d’un cône.
Formule de l’aire d’une boule et formule de l’aire d’un cône.
Il faut comparer le volume de la glace en forme de boule et le volume de la glace qui remplirait le cône à ras bord.
Question 2
Gabriel va d'abord calculer le volume de la glace en forme de boule, Quelle formule va-t-il utiliser ?
\(V = \dfrac{4}{3} \times \pi \times R^3\)
\(V = \dfrac{4}{3} \times \pi \times R^2\)
\(V = \dfrac{1}{3} \times \pi \times R^3\)
\(V = \dfrac{1}{3} \times \pi \times R^2\)
À connaître par cœur : le volume \(V\) d’une boule de rayon \(R\) est donné par la formule :\(V = \dfrac{4}{3} \times \pi \times R^3\).
Question 3

On a donc : \(V = \dfrac{4}{3} \times \pi \times R^3\).
Dans ce cas, quelle est la valeur exacte du volume de la glace ?
\(V = \dfrac{4}{3} \times \pi \times R^3 = \dfrac{4}{3} \times \pi \times 6^3 = 288\pi\) cm3
\(V = \dfrac{4}{3} \times \pi \times R^3 = \dfrac{4}{3} \times \pi \times 3^3 = 36\pi\) cm3
\(V = \dfrac{4}{3} \times \pi \times R^3 = \dfrac{4}{3} \times \pi \times 2,1^3 = 12,348\pi\) cm3
\(V = \dfrac{4}{3} \times \pi \times R^3 = \dfrac{4}{3} \times \pi \times 4,2^3 = 98,784\pi\) cm3
Le diamètre de la boule est de 6 cm, son rayon est donc de 3 cm.
Question 4

On a donc : \(V = 36 \pi\) cm3
Dans ce cas, quelle est la valeur arrondie au dixième du volume de la glace ?
\(V = 113\) cm3
\(V = 113,0\) cm3
\(V = 113,1\) cm3
\(V = 113,09\) cm3
Arrondir au « dixième » signifie qu’il y aura un seul chiffre à droite de la virgule.
Mais pour faire l’arrondi, il faut considérer la décimale suivante, c’est-à-dire ici celle des centièmes.
Ici c’est « 9 », il faut donc prendre la valeur approchée au dixième par excès.
Question 5

Gabriel va ensuite calculer le volume de la glace si on en remplit le cône.
Quelle formule va-t-il utiliser ?
\( V = 2\pi R \times h\)
\( V = 2\pi R^2 \times h\)
\( V = \dfrac{4}{3} \times \pi R^2 \times h\)
\( V = \dfrac{1}{3} \times \pi R^2 \times h\)
À connaître par cœur : le volume \(V\) d’un cône de hauteur \(h\) et de rayon de base \(R\) est donné par la formule : \( V = \dfrac{1}{3} \times \pi R^2 \times h\).
Question 6

On a donc : \( V = \dfrac{1}{3} \times \pi R^2 \times h\).
Dans ce cas, quelle est la valeur exacte du volume de la glace si on en remplit le cône ?
\( V = \dfrac{1}{3} \times \pi R^2 \times h = \dfrac{1}{3} \times \pi \times 4,2^2 \times 12 = 70,56\pi\) cm3
\( V = \dfrac{1}{3} \times \pi R^2 \times h = \dfrac{1}{3} \times \pi \times 2,1^2 \times 12 = 17,64\pi\) cm3
\( V = \dfrac{1}{3} \times \pi R^2 \times h = \dfrac{1}{3} \times \pi \times 3^2 \times 12 = 36\pi\) cm3
\( V = \dfrac{1}{3} \times \pi R^2 \times h = \dfrac{1}{3} \times \pi \times 6^2 \times 12 = 144\pi\) cm3
Le diamètre du cercle de base est de 4,2 cm, son rayon est donc de 2,1 cm.
Question 7

\(V = 17,64\) cm3.
Dans ce cas, quelle est la valeur, arrondie au dixième, du volume de la glace, si on en remplit le cône ?
\(V = 55,3\) cm3
\(V = 55,4\) cm3
\(V = 55,5\) cm3
\(V = 55,42\) cm3
Arrondir au « dixième » signifie qu’il y aura un seul chiffre à droite de la virgule.
Mais pour faire l’arrondi, il faut considérer la décimale suivante, c’est-à-dire ici celle des centièmes.
Ici c’est « 1 », il faut donc prendre la valeur approchée au dixième par défaut.
Question 8
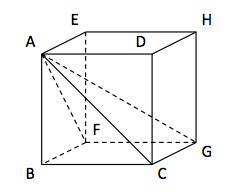
\(ABCDEFGH\) est un cube d'arête 6 cm.
Dans un premier temps, on veut calculer la longueur \(AC\), pour cela, on va utiliser le théorème de Pythagore dans le triangle \(ABC\) rectangle en \(B\).
Quelle est la valeur exacte de \(AC\) ?
\(AC^2 = AB^2 + BC^2\) ce qui donne \(AC^2 = 36\) et pour terminer \(AC = 6\) cm
\(AC^2 = AB^2 + BC^2\) ce qui donne \(AC^2 = 72 \) et pour terminer \(AC =\sqrt{72}\) cm
\(AC^2 = AB^2 + BC^2\) ce qui donne \(AC^2 = 72 \) et pour terminer \(AC = 8,4\) cm
\(AC^2 = AB^2 + BC^2\) ce qui donne \(AC^2 = 36\) et pour terminer \(AC = 8,485281374 \) cm
Pas de difficulté ici, attention de bien garder la valeur exacte et d’éviter de passer à des valeurs approchées.
\(AC^2 = AB^2 + BC^2 = 6^2 + 6^2 = 36 + 36 = 72 \)
Pour terminer \(AC =\sqrt{72}\) cm.
Question 9

\(ABCDEFGH\) est un cube d'arête 6 cm.
On admettra que le triangle \(ACG\) est rectangle en \(C\).
Quelle est la valeur exacte de \(AG\) ?
\(AG^2 = AC^2 + CG^2\) ce qui donne \( AG^2 = 108\) et pour terminer \(AG = \sqrt{108} \) cm
\(AG^2 = AC^2 + CG^2\) ce qui donne \( AG^2 = 5220\) et pour terminer \(AG = \sqrt{5220} \) cm
\(AG^2 = AC^2 + CG^2\) ce qui donne \( AG^2 = 108\) et pour terminer \(AG = 10,4 \) cm
\(AG^2 = AC^2 + CG^2\) ce qui donne \( AG^2 = 108\) et pour terminer \(AG = 10,39230485 \) cm
Encore une fois : dans un triangle rectangle : c’est le théorème de Pythagore qui va t’aider.
\(AG^2 = AC^2 + CG^2 = 6^2 + \sqrt{72}^2 = 36 + 72 = 108 \)
Pour terminer \(AG = \sqrt{108}\) cm.
Question 10

\(ABCDEFGH\) est un cube d'arête 6 cm.
On considère la pyramide \(ABCGF\).
Quel est le volume de cette pyramide ?
\( V = \dfrac{1}{3} \times\) Aire de la base \( \times h = \dfrac{1}{3} \times 6^2 \times 6 = 24\) cm3
\( V = \dfrac{1}{3} \times\) Aire de la base \( \times h = \dfrac{1}{3} \times 6^2 \times \sqrt{72} = 12 \sqrt{72} = 12\times 6 \sqrt{2} = 72 \sqrt{2}\) cm3
\( V = \dfrac{1}{3} \times\) Aire de la base \( \times h = \dfrac{1}{3} \times 6\times 6 = 12\) cm3
\( V = \dfrac{1}{3} \times\) Aire de la base \( \times h = \dfrac{1}{3} \times 6^2 \times 6 = 72\) cm3
À connaître par cœur : le volume \(V\) d’une pyramide de hauteur \(h\) est donné par la formule : \( V = \dfrac{1}{3} \times\) Aire de la base \( \times h \).
Et la hauteur mesure aussi 6 cm.
Ici, la base est un carré de côté 6 cm.
