Fiche de cours
Les 4 opérations - Additions et soustractions
L'addition
Une addition signifie ajouter et le résultat d'une addition est une somme.
Exemples
On me donne 3 livres. Le lendemain, on me donne 5 livres. On se demande combien de livres on possède.
Pour cela, on effectue l'addition suivante $ 3 + 5 = 8$.
On possède donc 8 livres.
Je parcours 12 km puis 10 km. Combien de kilomètres au total ai je parcouru ?
On a donc parcouru
$12 + 10 = 22$ km.
Soient $A$, $B$ et $C$ trois points alignés tels que $B \in [AC]$,
On suppose que l'on connait les longueurs $AB$ et $BC$ et on souhaite déterminer la longueur $AC$. 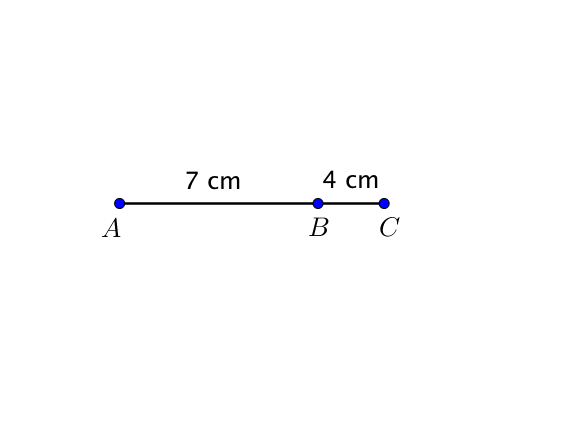
Ainsi, $AC = AB + BC$ car les points sont alignes.
Donc
$AC = 7 + 4 = 11$ cm.
La soustraction
Soustraire signifie retirer, enlever. Le résultat d'une soustraction est une différence.
Exemples
Je possède 15 livres et j'en donne 4. J'en aurai donc 4 en moins. Combien de livres me reste t il ?
J'enlève donc 4 livres aux 15 que je possédais initialement. Il me reste alors
$15 - 4 = 11$ livres
Léo a parcouru 16 km et Alice a parcouru 12 km. On souhaite donc comparer la distance qu'ils ont parcouru. Léo a parcouru plus de kilomètres qu'Alice ou Alice a parcouru moins de kilomètres que Léo. On se demande combien de kilomètre Léo a t il parcouru en plus, c'est à dire la différence.
On calcule donc la différence $16 - 12$. Pour cela, on peut se demande combien il faut ajouter à 12 pour atteindre 16.
Finalement, $16 - 12 = 4$.
Ainsi, Léo a parcouru 4 km de plus qu'Alice.
Soient $I$, $J$ et $K$ trois points alignés dans cet ordre tels que $B \in [AC]$,
On suppose que l'on connait $IJ$ et $IK$ et on souhaite trouver $JK$.
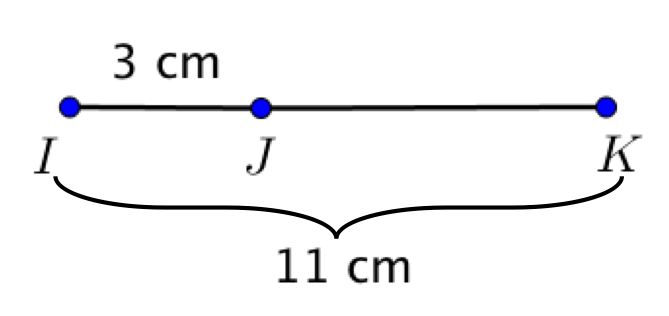
On cherche donc ce qu'il manque à 3 pour parvenir à 11.
C'est à dire on souhaite calculer la différence $11 - 3$ ou bien se demander quel nombre il faut ajouter à 3 pour atteindre 11 :
$11 - 3 = 8$
Ainsi, $JK = 8$.
