L'énoncé
Le but de cet exercice est de déplacer le scarabée sur le trajet grisé en complétant l'algorithme existant. Tout déplacement laissera une trace rouge sur la figure.
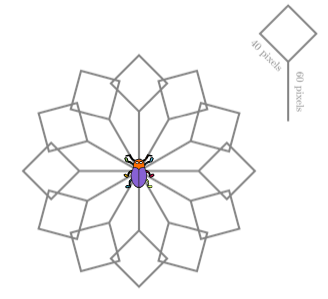

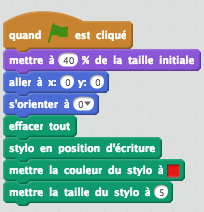
Question 1
Ouvrir Scratch en cliquant sur ce lien, un nouvel onglet s'ouvrira.
Nous allons commencer par créer notre motif qui sera répété 12 fois pour réaliser la figure.
Pour cela, créer un bloc (rubrique "Bloc" en violet) que l'on nommera "Motif".
Ajouter le premier segment mesurant 60 pixels du motif.
Glisser le bloc "Motif" dans l'algorithme.
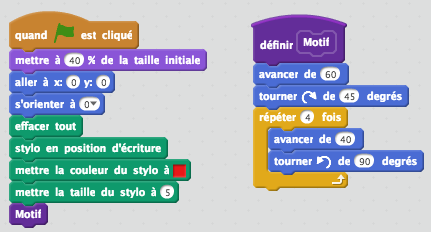
Voici l'algorithme complété :
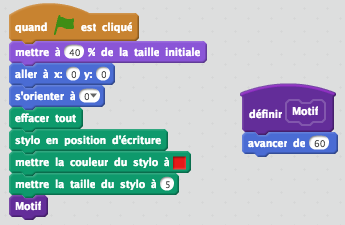
Le motif n'est pas accroché au reste de l'algorithme, c'est normal.
Il faut en revanche ajouter le bloc "motif" dans l'algorithme.
Question 2
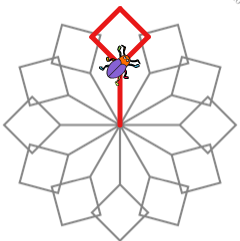
Le scarabée est dans cette position :
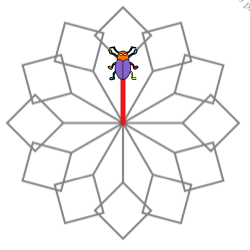
Il va falloir tourner d'un certain angle puis construire un carré de côté 40 pixels.
Ajouter les commandes dans le bloc "motif".
Après avoir avancé de 60 pixels on tourne de $45°$ à droite par exemple.
On crée à présent un carré en répétant 4 fois la même action.
On obtient :
Penser à des symétries pour trouver l'angle de rotation.
Penser à utiliser la commande "Répéter" pour le carré.
Question 3
Le carré est tracé mais le scarabée est mal orienté.
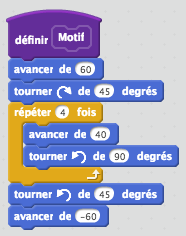
Ajouter les deux blocs nécessaires pour le faire pivoter et le recentrer.
Il faut revenir au point de départ donc :
- Tourner à gauche de $45°$
- Reculer de 60 pixels (ou avancer de -45 pixels)
On rebrousse chemin !
On commence par tourner à gauche puis reculer.
Question 4
Le motif est terminé et le scarabée est à présent dans cette position.
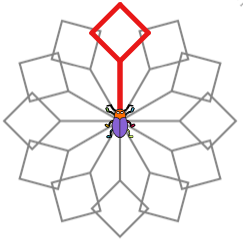
Il va falloir faire pivoter le scarabée puis répéter 12 fois le motif.
Compléter l'algorithme pour finir la figure.
Il faut répéter 12 fois le même motif donc on cherche l'angle de rotation :
$x=\dfrac{360}{12}=30°$
On obtient donc :
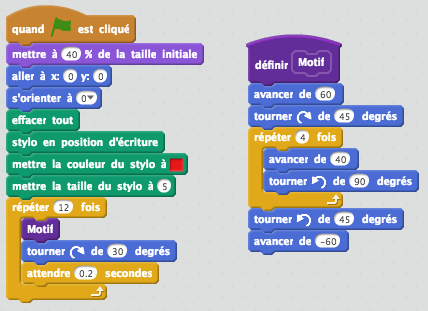
Calculer l'angle de rotation pour commencer.
On partage un angle plein mesurant $360°$ en $12$ parts égales.
