L'énoncé
Le but de cet exercice est de déterminer un algorithme qui permet de dire si un nombre est divisible par $7$ ou non.
Pour rappel, un nombre est divisible par $7$ si le reste de la division euclidienne de ce nombre par $7$ vaut $0$.
Exemples :
$84=12\times 7+0$ Le reste de la division vaut $0$ donc $84$ est divisible par $7$.
$115=16 \times 7 +3$ Le reste de la division vaut $3$ donc $115$ n'est pas divisible par $7$.
Dans Scratch, le bloc qui donne le reste d'une division euclidienne est MODULO : 
Ici, $115$ modulo $7$ sera égal au nombre $3$, le reste de la division de $115$ par $7$.
Question 1
Créer le début de l'algorithme avec Scratch qui permet de demander à l'utilisateur de saisir un nombre.
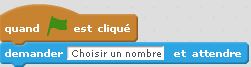
Question 2
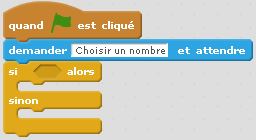
Ajouter un bloc qui permettra ensuite de tester si le nombre est divisible par $7$ ou non.
Il y aura deux réponses possibles à cette question : oui ou non.
Question 3
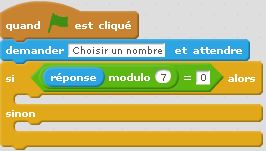
Compléter le champ qui vient après "SI".
On veut tester la valeur du reste de la division euclidienne du nombre saisi par 7.
Dans Scratch, la réponse de l'utilisateur est : 
C'est la partie difficile : On se demande si le reste de la division de "réponse" par $7$ vaut $0$ ou non.
Question 4
Terminer l'algorithme en écrivant le texte adapté dans les zones "Alors" et "sinon"

