Fiche de cours
Calculs sur les parallèles
I. La longueur d’un parallèle
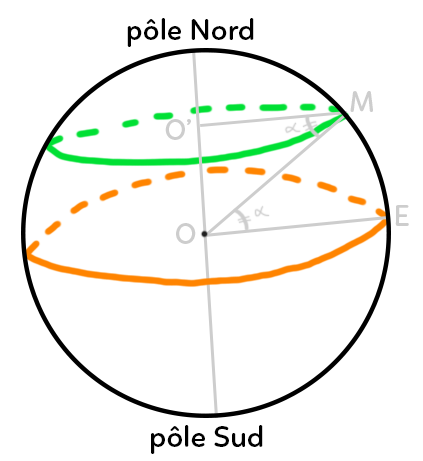
Dans ce schéma, il y a un parallèle représenté en vert et l’équateur représenté en orange. L’angle alpha se retrouve à deux endroits car on a des angles alternes-internes. Alpha étant la latitude.
Un parallèle est un cercle imaginaire. Sa longueur est donc la circonférence du cercle, dont la formule générale à connaître est : $l = 2\pi r$, avec $r$ le rayon.
Le rayon n’est pas le même pour le parallèle et pour l’équateur, étant donné la forme sphérique de la Terre. On cherche à exprimer ce rayon, donc la distance : $O’M$. On a $2\times \pi \times O’M$ avec $O’M$ exprimé en fonction des autres grandeurs sur le schéma.
Le triangle $OO’M$ est rectangle en $O’$ et on peut donc dire que dans ce triangle, le cosinus de alpha est égal à :
$\dfrac{côté \ adjacent}{hypothénuse}=\dfrac{O’M}{OM}$.
On peut en d
