Fiche de cours
I. Définition
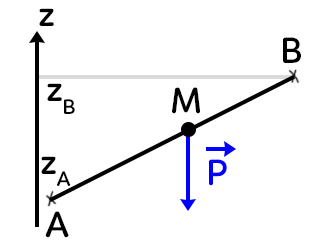
On s’intéresse à la force $P$ s’appliquant sur le point $M$ qui se déplace de $A$ à $B.$ L’énergie potentielle est exclusivement associée à une force conservative. On pourra donc associer une énergie potentielle $Ep$ à toute force conservative. La variation d’énergie potentielle se définit par :
$\Delta (Ep) = Ep(B)- Ep(A) = - WAB(P) = - m \times g \times (z_A- z_B) = m \times g \times (z_B-z_A)$
Le signe négatif vient du sens de $P$ qui est opposé à l’axe $z.$ On peut exprimer le poids en fonction de la masse et de la force de la gravitation.
II. Pas d’erreur de signe
Si l’altitude augmente dans le cas de l’énergie potentielle, alors cette dernière augmente et $\Delta Ep > 0$.
Si l’altitude diminue alors l’énergie potentielle diminue et $\Delta Ep < 0$.
$m$ et $g$ sont toujours positifs.
