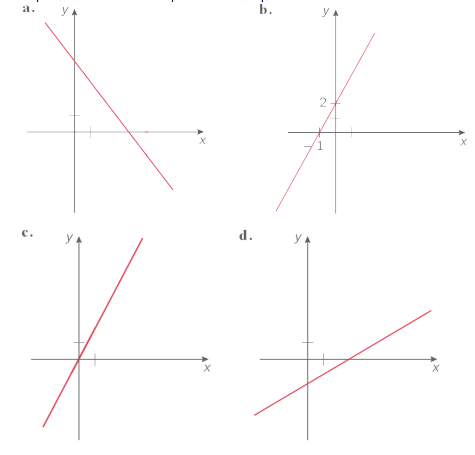
1) Soit l’équation cartésienne suivante : $2x – y + c = 0$ (avec $c$ quelconque).
Laquelle ou lesquelles de ces droites correspondent à cette équation ?
2) Soit la droite $d$ d’équation cartésienne $8x – 11y + 3 = 0$.
Citez les bonnes réponses et justifiez :
a) Un vecteur directeur de $d$ est $\vec{u}(−5,5; −4)$.
b) Un vecteur directeur de $d$ est $\vec{v}(−11; 8)$.
c) L’équation réduite de la droite est $y = 8x + \dfrac{3}{11}$.
d) Le point $A(0 ;4)$ appartient à $d$.
3) Soit la droite $d_1$ d’équation $4x+3y–5=0$ et la droite $d_2$ d’équation $y=6$.
Les affirmations suivantes sont-elles vraies ou fausses ? Justifiez.
a) La droite $d_2$ est parallèle à l’axe des abscisses.
b) Les droites $d_1$ et $d_2$ se coupent en $A\left(\dfrac{-13}{4}; 6\right)$.
c) La droite $d_1$ a comme vecteur directeur $\vec{u} (−9; 12)$.
2) Soit la droite $d$ d’équation cartésienne $8x – 11y + 3 = 0$.
a) Un vecteur directeur de $d$ est $\vec{u}(−5,5; −4)$.
Vrai, car c’est un vecteur colinéaire du vecteur $\vec{w}(11; 8)$ obtenu avec le théorème du cours selon lequel le vecteur directeur d’une droite définie par $ax + by + c = 0$ est $(–b ;a)$.
b) Un vecteur directeur de $d$ est $\vec{v}(−11; 8)$.
Faux : ce n’est pas un vecteur colinéaire de $\vec{w}(11; 8)$.
c) L’équation réduite de la droite est $y =8x +\dfrac{3}{11}$.
Faux : l’équation réduite de la droite est $y=\dfrac{8}{11}x+\dfrac{3}{11}$.
d) Le point $A(0 ;4)$ appartient à $d$.
Faux : remplaçons $x$ et $y$ par 0 et 4 :
$8×0−11×4+3=−44+3=−41 \neq 0$
Ainsi, $A(0;4)$ n’appartient pas à $d$.
3) Soit la droite $d_1$ d’équation $4x+3y–5=0$ et la droite $d_2$ d’équation $y=6$ :
a) La droite $d_2$ est parallèle à l’axe des abscisses.
Vrai. C'est une question de cours. Son coefficient directeur est nul.
b) Les droites $d_1$ et $d_2$ se coupent en $A\left(\dfrac{-13}{4}; 6\right)$.
Vrai, on résout le système d’équations suivant :
$\begin{equation*}\left\{\begin{aligned}y&=6& \\4x+3\,y-5&=0& \\\end{aligned} \right.\end{equation*}$
$\begin{equation*}\left\{\begin{aligned}y&=6& \\4x+3\times 6-5\,&=0& \\\end{aligned} \right.\end{equation*}$
$\begin{equation*}\left\{\begin{aligned}y&=6& \\4x+13\,&=0& \\\end{aligned} \right.\end{equation*}$
$\begin{equation*}\left\{\begin{aligned}y&=6& \\x\,&=\dfrac{-13}{4}& \\\end{aligned} \right.\end{equation*}$
c) La droite $d_1$ a comme vecteur directeur $\vec{u}(−9; 12)$.
Vrai, c’est un vecteur colinéaire de $\vec{v}(−3; 4)$.
