L'énoncé
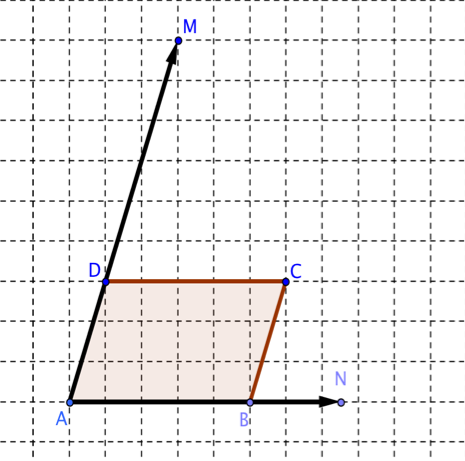
\(ABCD\) est un parallélogramme. Le point N est défini par : \( \vec{AN}=\dfrac{3}{2} \vec{AB} \) et le point M est défini par : \( \vec{DM}= 2 \vec{AD}\)
Tu as obtenu le score de
Question 1
La décomposition de \( \vec{CN}\) en fonction de \(\vec{AB}\) et \(\vec{AD}\) est :
\(\vec{CN}= \vec{AB} + \vec{AD}\)
\( \vec{CN}= \dfrac{1}{2} \vec{AB} - \vec{AD}\)
\(\vec{CN}=\dfrac{1}{2} \vec{AB} + \vec{AD}\)
\(\vec{CN}= \vec{AB} - \vec{AD}\)
Tout commence par une relation de Chasles…
On a : \(\vec{CN}= \vec{CA} + \vec{AN} \)
Utilise l’hypothèse de l’énoncé sur \(\vec{AN}\)
Il faut aussi utiliser la relation de Chasles sur \(\vec{CA} \)
on a \(\vec{CA}=\vec{CB} + \vec{BA}\)
On utilise la relation de Chasles sur \(\vec{CN}\) (dans le but ensuite d’utiliser les hypothèses de l’énoncé sur \(\vec{AN}\)… ce qui nous pousse à introduire le point A) :
\(\vec{CN}= \vec{CA} + \vec{AN} \)
\( \vec{CN} = \vec{CA} + \dfrac{3}{2}\vec{AB} \)
\( \vec{CN} = \vec{CB} + \vec{BA} + \dfrac{3}{2}\vec{AB}\)
\( \vec{CN} = \vec{DA} - \vec{AB} + \dfrac{3}{2}\vec{AB}\)
\(\vec{CN}= - \vec{AD} + \dfrac{1}{2} \vec{AB}\)
Donc on a bien : \(\vec{CN}= \dfrac{1}{2} \vec{AB} - \vec{AD} \)
Le plus des bons profs : On utilise souvent la relation de Chasles dans ce type de question. Une petite réflexion est nécessaire pour savoir quel point on choisit : par exemple dans le première relation de Chasles, j’utilise A car dans l’énoncé, la seule hypothèse sur N est contenue dans l’égalité sur le vecteur \(\vec{AN}\) : pour l’utiliser je dois donc fai
Question 2
La décomposition de \(\vec{CM} \) en fonction de \(\vec{AB} \) et \(\vec{AD} \) est :
\(\vec{CM}= - \vec{AB} +2 \vec{AD}\)
\(\vec{CM}= \dfrac{1}{2} \vec{AB} +2 \vec{AD}\)
\(\vec{CM}= \vec{AB} + \vec{AD}\)
\( \vec{CM}= \vec{AB} - 2\vec{AD}\)
Tout commence par une relation de Chasles…
On a : \(\vec{CM}= \vec{CD} + \vec{DM} \)
Utiliser l’hypothèse de l’énoncé sur \(\vec{DM}\)
On utilise la relation de Chasles sur \(\vec{CM}\) (dans le but ensuite d’utiliser les hypothèses de l’énoncé sur \(\vec{CM}\)… ce qui nous pousse à introduire le point D) :
\(\vec{CM}= \vec{CD} + \vec{DM} \)
\(\vec{CM} = \vec{BA} + 2 \vec{AD}\)
\(\vec{CM} = - \vec{AB} + 2\vec{AD}\)
Le plus des bons profs : Là aussi, on a commencé le calcul par la relation de Chasles. Tu vois que choisir D comme point à introduire grâce la relation de Chasles est bien pratique pour utiliser l’hypothèse : \(\vec{DM}= 2 \vec{AD}\)
Question 3
On peut déduire des questions 1 et 2 que :
\(\vec{CM}= 2 \vec{CN}\)
\(\vec{CM}= -2 \vec{CN}\)
\(\vec{CM}= -\dfrac{1}{2}\vec{CN}\)
Les points \(C\), \(M\) et \(N\) sont alignés.
Par quoi multiplier les coefficients de \(\vec{CN}\) pour obtenir ceux de \(\vec{CM}\) ?
Il s’agit là de mettre en relation les égalités :
\(\vec{CN}= \dfrac{1}{2} \vec{AB} - \vec{AD} \) et \( \vec{CM}= - \vec{AB} +2 \vec{AD}\)
On va multiplier par \((-2)\) la première égalité :
\(\vec{CN}= \dfrac{1}{2} \vec{AB} - \vec{AD}\)
\( \Leftrightarrow(-2) \times \vec{CN}= (-2) \times \dfrac{1}{2} \vec{AB} – (-2) \times \vec{AD}\)
\(\Leftrightarrow -2\vec{CN} =- \vec{AB} + 2\vec{AD}\)
Et on reconnaît ici le vecteur \( \vec{CM}\).
Donc \(\vec{CM}= -2\vec{CN}\).
Cela prouve que les vecteurs \(\vec{CM}\) et \(\vec{CN} \) sont colinéaires, donc les points \(C\), \(M\) et \(N\) sont alignés.
Question 4
On se place dans le repère \((A; \vec{AB};\vec{AD} )\).
Les coordonnées de N dans ce repère sont : \(N\left(0 ;\dfrac{3}{2}\right)\)
Les coordonnées de N dans ce repère sont : \(N\left(\dfrac{3}{2} ;0\right)\)
Les coordonnées de M dans ce repère sont : \(M(0 ;3)\)
Les coordonnées de M dans ce repère sont :\( M(3 ;0)\)
Un coup d’œil à la figure devrait pouvoir t’aider
Pour justifier ces affirmations dans un contrôle, il faut utiliser des décompositions, et ne pas se contenter de lectures graphiques (voir les commentaires pour la rédaction ).
Voici comment rédiger la recherche de ces coordonnées lors d’un contrôle :
Pour \(\vec{AN}\) : c’est immédiat car \( \vec{AN}= \frac{3}{2} \vec{AB}\) donc les coordonnées de \(N \)sont \((\frac{3}{2} ;0)\)
Pour \( \vec{AM}\) : On décompose \(\vec{AM} \) en fonction de \(\vec{AB}\) et de \( \vec{AD}\).
\(\vec{AM} = \vec{AD} + \vec{DM}\)
\( \vec{AM} = \vec{AD} + 2 \vec{AD}\)
\(\vec{AM} = 3 \vec{AD} \)
Donc les coordonnées de \(M \)sont (\(0 ;3)\).
Le plus des bons profs :
Attention à l’ordre des coordonnées : il faut respecter l’ordre de l’écriture du repère \((A, \vec{AB},\vec{AD} )\)
Comme \(\vec{AD}\) est le deuxième vecteur, le coefficient 3 correspond à la deuxième coordonnée.
Question 5
On se place encore dans le repère \( (A, \vec{AB},\vec{AD} )\). Une équation de la droite \( (MN\)) dans ce repère est :
\(6x+3y-9 =0\)
\(-6x-3y+9 =0\)
\(6x-3y-9 =0\)
\(6x+3y+9 =0\)
On va utiliser le critère de colinéarité. Commence par trouver les coordonnées de \( \vec{MN}\) avec la formule \( \vec{MN}(x_N-x_M;y_N-y_M)\)
Un point \(P\) de coordonnées \( (x ;y)\) appartient à \( (MN)\) si et seulement si \(\vec{ NP}\) et \( \vec{MN}\) sont colinéaires… Puis on applique le critère de colinéarité.
Un point P de coordonnées \((x ;y)\) appartient à \((MN)\) si et seulement si\( \vec{ NP}\) et \(\vec{MN}\) sont colinéaires. On a :
\(\vec{ NP}(x-\dfrac{3}{2};y)\) et \(\vec{MN}(\dfrac{3}{2}; 3)\)
\(\vec{ NP}\) et \(\vec{MN}\) colinéaires \(\Leftrightarrow 3(x-\dfrac{3}{2})-\dfrac{3}{2}y=0\) (c’est le critère de colinéarité)
\(\Leftrightarrow -3x+\dfrac{9}{2}=\dfrac{3}{2}y\)
\(\Leftrightarrow -6x - 3y + 9 = 0\)
Le plus des Bons Profs :
On peut, à partir de l’équation \(6x+3y-9 =0\), montrer (par une autre méthode) que les points \( C\), \( M\) et \( N\) sont alignés : les coordonnées de \(C\) dans le repère \( (A, \vec{AB},\vec{AD} )\) sont \( C(1 ;1\)).
On remplace alors dans l’équation : \(6\times1+3\times1-9 =9-9=0\)
Les coordonnées de \(C\) vérifient une équation de \( (MN\)) donc \(C\) appartie
