L'énoncé
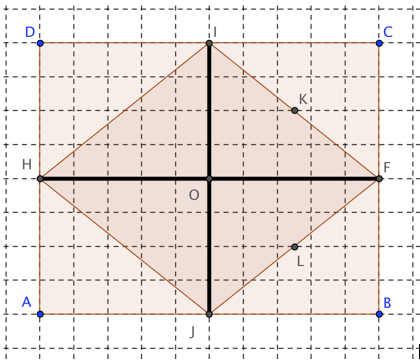
Dans tout cet exercice, on utilise la figure suivante : \(ABCD\) est un rectangle, \(I, J, H\) et \(F\) sont les milieux des 4 cotés. On admet qu’ils forment un parallélogramme. \(K\) est le milieu de \([ IF]\) et \(L\) est le milieu de \([JF]\).
Tu as obtenu le score de
Question 1
On se place dans le repère \((A,\overrightarrow{AB},\overrightarrow{AD} )\).
Les coordonnées de \(B\) sont \((1 ;0)\).
Les coordonnées de \(B\) sont \((1 ;-1)\).
Les coordonnées de \(C\) sont \((1 ;1)\).
Les coordonnées de \(O\) sont \((0,5 ;0,5)\).
C’est une simple lecture du graphique : \(\overrightarrow{AB}\) est le premier vecteur de la base (donc la longueur \(AB\) donne l’unité de longueur sur cet axe).
On peut faire référence à la définition du cours : \(\overrightarrow{AB}= 1 \overrightarrow{AB} + 0\overrightarrow{AD}\) : les coefficients sont alors les coordonnées de \(B\). Faites la même chose pour les autres points.
\( \overrightarrow{AC}= 1 \overrightarrow{AB} + 1 \overrightarrow{AD}\) donc les coordonnées de \(C\) sont…
\(\overrightarrow{AO}= 0,5 \overrightarrow{AB} + 0,5 \overrightarrow{AD}\) donc les coordonnées de \(O\) sont...
On peut faire référence à la définition du cours : \(\overrightarrow{AB}= 1 \overrightarrow{AB} + 0\overrightarrow{AD}\) : les coefficients sont alors les coordonnées de \(B\). Faites la même chose pour les autres points.
\( \overrightarrow{AC}= 1 \overrightarrow{AB} + 1 \overrightarrow{AD}\) donc les coordonnées de \(C\) sont…
\(\overrightarrow{AO}= 0,5 \overrightarrow{AB} + 0,5 \overrightarrow{AD}\) donc les coordonnées de \(O\) sont...
Beaucoup de ces coordonnées peuvent être lues directement sur la figure. Mais vous devez savoir que derrière ces lectures, il y a l’idée que l’on décompose chaque vecteur en fonction de \(\overrightarrow{AB}\) et \(\overrightarrow{AD}\).
Par exemple \(\overrightarrow{AO}= 0,5 \overrightarrow{AB} + 0,5 \overrightarrow{AD}\) permet d’affirmer que les coordonnées de \(O\) sont \((0,5 ;0,5)\).
Question 2
On se place dans le repère \((J, \ \overrightarrow{JF}, \overrightarrow{JH})\).
Les coordonnées de \(J\) sont \((0 ;0)\).
Les coordonnées de \(J\) sont \((0 ;0)\) (c’est l’origine du repère) : la proposition est juste.
Les coordonnées de \(F\) sont \((1 ;0)\).
\( \overrightarrow{JF} = 1 \overrightarrow{JF} + 0 \overrightarrow{JH} \)
Les coordonnées de \(H\) sont \((0 ;1)\).
\( \overrightarrow{JH} = 0 \overrightarrow{JF} + 1 \overrightarrow{JH} \)
Les coordonnées de \(L\) sont \((0,5 ;0,5)\).
Les coordonnées de \(L\) sont \((0,5 ; 0)\) car \(\overrightarrow{JL} = 0,5 \overrightarrow{JF} + 0 \overrightarrow{JH}\). La proposition est fausse.
Visualisez le repère : l’origine est \(J\) et le axes sont les droites \((JF)\) et \((JH)\). Cela doit vous permettre de contrôler les propositions 1, 2 et 3 ! Sinon une petite décomposition en fonction des vecteurs \( \overrightarrow{JF}\) et \(\overrightarrow{JH} \)...
Décomposez le vecteur \(\overrightarrow{JL}\) en fonction des deux vecteurs de base \(\overrightarrow{JF}\) et \(\overrightarrow{JH}\).
Décomposez le vecteur \(\overrightarrow{JL}\) en fonction des deux vecteurs de base \(\overrightarrow{JF}\) et \(\overrightarrow{JH}\).
Question 3
On se place encore dans le repère \((J, \overrightarrow{JF}, \overrightarrow{JH})\).
Les coordonnées de \(I\) sont \((1 ;1)\).
Les coordonnées de \(O\) sont \((0 ;0)\).
La décomposition de \(\overrightarrow{JO}\) selon \(\overrightarrow{JF}\) et \(\overrightarrow{JH}\) est :
\(\overrightarrow{JO} = 0,5 \overrightarrow{JF} + 0,5 \overrightarrow{JH}\)
Les coordonnées de \(O\) sont \((0,5 ;0,5)\).
Pour la proposition 1 : \( \overrightarrow{JI} = 1 \overrightarrow{JF} + 1 \overrightarrow{JH}\) donc...
Pour la proposition 3 : \(\overrightarrow{JO} = 0,5 \overrightarrow{JI}\) puis remplacer \(\overrightarrow{JI}\) par sa décomposition.
Pour la proposition 3 : \(\overrightarrow{JO} = 0,5 \overrightarrow{JI}\) puis remplacer \(\overrightarrow{JI}\) par sa décomposition.
On a les décompositions suivantes :
- \( \overrightarrow{JI}= 1 \overrightarrow{JF} + 1 \overrightarrow{JH} \) donc les coordonnées de \(I\) sont \((1 ;1)\).
- \( \overrightarrow{JO} = 0,5\overrightarrow{JI}=0,5 ( \overrightarrow{JF} + \overrightarrow{JH}) = 0,5 \overrightarrow{JF} + 0,5\overrightarrow{JH}\)
- Donc les coordonnées de \(O \) sont \((0,5 ;0,5)\).
Question 4
On se place encore dans le repère \((J, \overrightarrow{JF}, \overrightarrow{JH})\). Les coordonnées de \(K\) sont :
\((0 ;1,5)\)
\((1 ;-0,5)\)
\((1 ;0,5)\)
\((0,5 ; 0,5)\)
Il faut trouver la décomposition de \(\overrightarrow{JK}\) en fonction de \(\overrightarrow{JF}\) et \(\overrightarrow{JH}\).
Relation de Chasles pour commencer : \(\overrightarrow{JK}= \overrightarrow{JF} + \overrightarrow{FK} \)
\( \overrightarrow{FK} = 0,5 \overrightarrow{FI} \)
Que dire de \(\overrightarrow{FI}\) et \( \overrightarrow{JH}\) ?
Relation de Chasles pour commencer : \(\overrightarrow{JK}= \overrightarrow{JF} + \overrightarrow{FK} \)
\( \overrightarrow{FK} = 0,5 \overrightarrow{FI} \)
Que dire de \(\overrightarrow{FI}\) et \( \overrightarrow{JH}\) ?
Pour trouver les coordonnées de \(K \): on cherche une décomposition de \(\overrightarrow{JK}\) en fonction de \(\overrightarrow{JF} \) et \( \overrightarrow{JH}\). Pour cela, on écrit :
\(\overrightarrow{JK}= \overrightarrow{JF} + \overrightarrow{FK}\) (relation de Chasles)
\( = \overrightarrow{JF} + 0,5 \overrightarrow{FI} \)
\( = 1 \overrightarrow{JF} +0,5 \overrightarrow{JH} \)
\(\overrightarrow{JK} = 1 \overrightarrow{JF} + 0,5 \overrightarrow{JH}\) donc \(K(1 ;0,5)\)
Cette méthode est à retenir !
\(\overrightarrow{JK}= \overrightarrow{JF} + \overrightarrow{FK}\) (relation de Chasles)
\( = \overrightarrow{JF} + 0,5 \overrightarrow{FI} \)
\( = 1 \overrightarrow{JF} +0,5 \overrightarrow{JH} \)
\(\overrightarrow{JK} = 1 \overrightarrow{JF} + 0,5 \overrightarrow{JH}\) donc \(K(1 ;0,5)\)
Cette méthode est à retenir !
Question 5
On se place dans le repère \((I, \overrightarrow{IF}, \overrightarrow{IH} )\). Les coordonnées de \( L\) sont :
\((0,5 ;1,5)\)
\((1 ;0,5)\)
\((1 ;-0,5)\)
\((0,5 ; 0,5)\)
Il faut trouver la décomposition de
\(\overrightarrow{IL}\) en fonction de \(\overrightarrow{IF}\) et \(\overrightarrow{IH}.\)
Relation de Chasles pour commencer : \( \overrightarrow{IL}= \overrightarrow{IF} + \overrightarrow{FL} \)
\( \overrightarrow{FL} = 0,5 \overrightarrow{FJ} \) et on a \(\overrightarrow{FJ} = \overrightarrow{IH}\)
Relation de Chasles pour commencer : \( \overrightarrow{IL}= \overrightarrow{IF} + \overrightarrow{FL} \)
\( \overrightarrow{FL} = 0,5 \overrightarrow{FJ} \) et on a \(\overrightarrow{FJ} = \overrightarrow{IH}\)
On trouve que : \(\overrightarrow{IL}= \overrightarrow{IF} + \overrightarrow{FL} = \overrightarrow{IF} +0,5 \overrightarrow{IH}\).
Les coordonnées de \(L\) sont donc : \(L(1 ; 0,5)\).
