L'énoncé
Trois dés cubiques sont placés dans une urne.
Deux de ces dés sont normaux : leurs faces sont numérotées de 1 à 6. Le troisième est spécial : trois de ses faces sont numérotées 6, les trois autres sont numérotés 1.
On tire de l’urne simultanément et au hasard, deux dés parmi les trois et on les lance.
On note A l’évènement : « Les deux dés tirés sont normaux. »
On note B l’évènement : « Les deux faces supérieures sont numérotées 6. »
Question 1
Définir l'événement contraire de \(A\) noté \(\overline{A}\).
\(\overline{A}\) : « Un des deux dés tirés est spécial. »
Si vous ne savez pas ce qu’est l’évènement contraire, relisez votre cours ou regardez la vidéo disponible dans les prérequis.
Question 2
Calculer les probabilités de \(A\) et de \(\overline{A}\).
Voici l'arbre de probabilité permettant de déterminer la probabilité de $A$
On note $N$ :" le dé est normal"

\(P(A)=\dfrac{2}{3}\times \dfrac{1}{2}\)
\(P(A)=\dfrac{1}{3}\)
En passant par l'événement contraire,
\(P(\overline{A})=1-p(A)=\dfrac{2}{3}\)
Combien y a-t-il de façon de choisir 2 dés parmi 3 ?
Combien y a-t-il de façon de choisir les 2 dés normaux ?
Question 3
Calculer \(P_A(B)\), probabilité de \(B\) sachant \(A\), puis \(P(B \cap A)\).
Sachant que les dés sont normaux, il y a \(36\) issues à cette expérience aléatoire. Une seule issue donne un double \(6\).
\(P_A(B)=\dfrac{1}{6}\times \dfrac{1}{6}=\dfrac{1}{36}\)
\(P(B \cap A)=P_A(B)\times P(A)=\dfrac{1}{36}\times \dfrac{1}{3}=\dfrac{1}{108}\)
C’est une probabilité conditionnelle, mais vous n’avez pas besoin d’utiliser la formule.
Sachant que les 2 dés tirés sont normaux, la probabilité que les faces supérieures soient numérotées 6 est facile à calculer.
Maintenant, on peut déduire de la formule la valeur de \(P(B \cap A)\).
Un trou de mémoire ? Regardez la vidéo sur les probabilités conditionnelles.
Question 4
Représenter le problème par un arbre de probabilités et calculer \(P(B)\).
L'arbre de probabilité est :
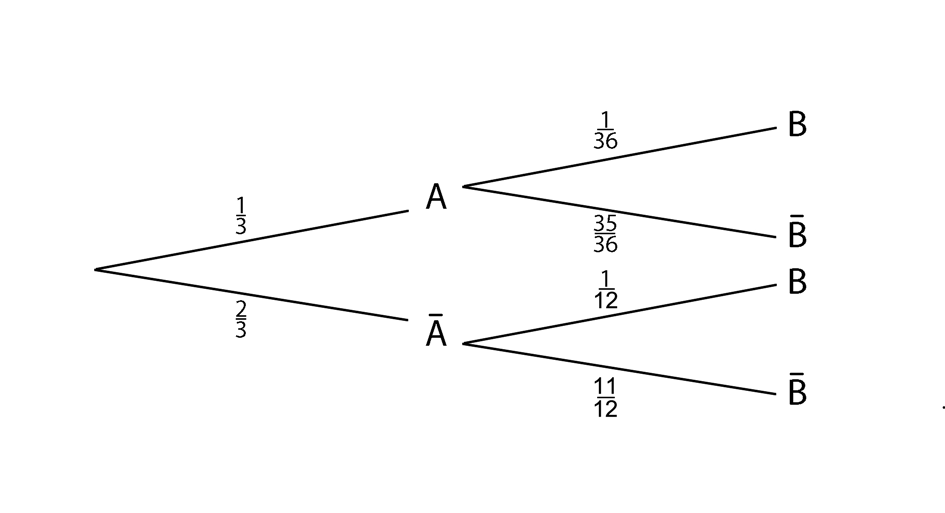
$A$ et $\overline A$ forment une partition de l'univers donc d'après la formule de probabilités totales,
\(P(B)=p(A)\times P_A(B)+p(\overline A)\times P_{\overline A}(B)\)
\(P(B)=\dfrac{1}{3}\times\dfrac{1}{36}+\dfrac{2}{3}\times\dfrac{1}{12}\)
\(P(B)=\dfrac{1}{108}+\dfrac{1}{18}\)
\(P(B)=\dfrac{7}{108}\)
Il faut envisager les 2 cas : soit les 2 dés sont normaux, soit l’un des 2 est spécial. Dans ce second cas, il y a une chance sur deux d’obtenir un 6 pour le dé spécial.
Question 5
Calculer \(P_B(A)\), probabilité de \(A\) sachant \(B\).
D'après le cours, on a :
\(P_B(A)=\dfrac{P(A \cap B)}{P(B)}\)-
\(P_B(A)=\dfrac{1}{108}\times\dfrac{108}{7}\)-
\(P_B(A)=\dfrac{1}{7}\)
Il suffit d’appliquer la formule !
