L'énoncé
Répondre aux questions suivantes, il y a qu'une bonne réponse par question.
Tu as obtenu le score de
Question 1
Trouver les racines du polynôme $P(x)=3x^2-2x-1$. On pourra chercher une racine évidente.
$x_1=\dfrac{-1}{3}$ et $x_2=\dfrac{1}{3}$
$x_1=\dfrac{-1}{3}$ et $x_2=1$
$x_1=3$ et $x_2=1$
$x_1=3$ et $x_2=\dfrac{1}{3}$
On remarque que $3-2-1=0$, donc $1$ est solution évidente.
On remarque que $3-2-1=0$, donc $1$ est une racine évidente.
On utilise le produit des deux racines $x_1\times x_2=\dfrac{c}{a}$
On en déduit :
$1\times x_2=\dfrac{-1}{3}$
alors $x_2=\dfrac{-1}{3}$
Question 2
Trouver les racines de $P(x)=2x^2-8x-2$.
$x_1=\dfrac{8+\sqrt{48}}{4}$ et $x_2=\dfrac{8-\sqrt{48}}{4}$.
$x_1=\dfrac{8+\sqrt{48}}{2}$ et $x_2=\dfrac{8-\sqrt{48}}{2}$.
$x_1=\dfrac{-8+\sqrt{48}}{4}$ et $x_2=\dfrac{-8-\sqrt{48}}{4}$.
$x_1=\dfrac{-8+\sqrt{48}}{2}$ et $x_2=\dfrac{8+\sqrt{48}}{2}$.
Le discriminant est $\Delta=48$
Le discriminant est $\Delta=48$.
Donc les racines sont
$x_1=\dfrac{8+\sqrt {48}}{4}$ et
$x_2=\dfrac{8-\sqrt{48}}{4}$.
Question 3
Factoriser $P(x)=2x^2+9x-7$.
$P(x)=\left(x+\dfrac{-9+\sqrt{137}}{4}\right) \times\left(x-\dfrac{-9-\sqrt{137}}{4}\right)$.
$P(x)=\left(x-\dfrac{-9+\sqrt{137}}{4}\right) \times\left(x-\dfrac{-9-\sqrt{137}}{4}\right)$.
$P(x)=\left(x-\dfrac{-9+\sqrt{137}}{4}\right)^2$.
$P(x)=\left(x+\dfrac{-9-\sqrt{137}}{4}\right) \times\left(x-\dfrac{-9-\sqrt{137}}{4}\right)$.
Le discriminant est $\Delta=137$.
On peut factoriser un trinôme ayant deux racines distinctes.
Le discriminant est $\Delta=137$.
Donc les racines sont $x_1=\dfrac{-9+\sqrt {137}}{4}$ et $x_2=\dfrac{-9-\sqrt{137}}{4}$.
Donc $P(x)=\left(x-\dfrac{-9+\sqrt{137}}{4}\right) \times\left(x-\dfrac{-9-\sqrt{137}}{4}\right)$.
Question 4
Donner les racines du polynôme représenté par la courbe $C_f$.
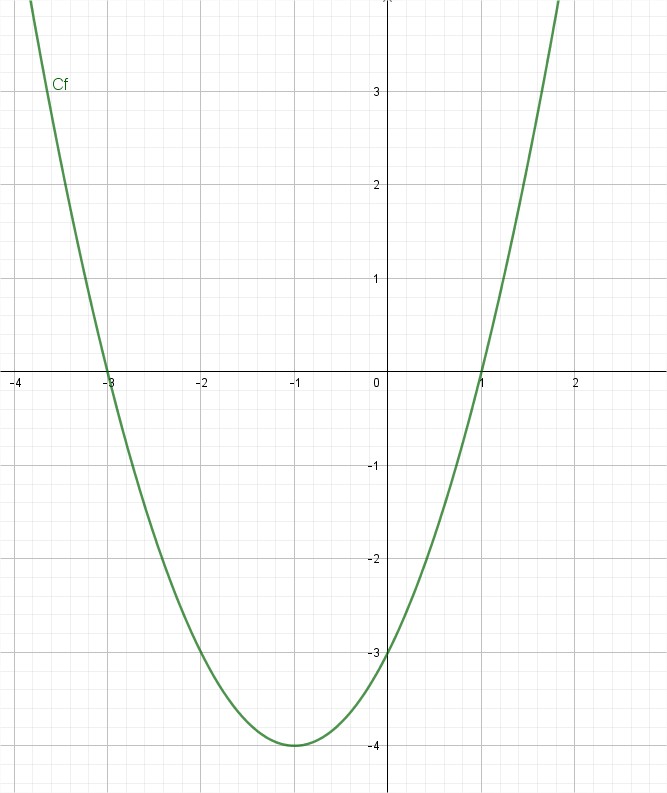
Les racines sont $1$ et $-3$.
Les racines sont $3$ et $-1$.
Les racines sont $-1$ et $-3$.
Les racines sont $1$ et $3$.
Les racines sont tels que $f(x)=0$.
Les racines sont $1$ et $-3$.
Ce sont les abscisses des points d'intersection de la courbe avec l'axe des abscisses
Question 5
Trouver les racines de $P(x)=9x^2-5x-4$. On cherchera une racine évidente.
$x_1=\dfrac{4}{9}$ et $x_2=\dfrac{5}{9}$
$x_1=1$ et $x_2=\dfrac{4}{9}$
$x_1=1$ et $x_2=\dfrac{-4}{9}$
$x_1=\dfrac{4}{5}$ et $x_2=\dfrac{5}{9}$
Faire la somme des coefficients de $P$.
On remarque $9-5-4=0$ donc $1$ est une solution évidente.
On utilise le produit des deux racines $x_1\times x_2=\dfrac{c}{a}$
On en déduit :
$1\times x_2=\dfrac{-4}{9}$
L'autre solution est alors $\dfrac{-4}{9}$.
Question 6
Trouver les racines de $P(x)=2x^2+5x+7$.
$x_1=\dfrac{2}{56}$ et $x_2=\dfrac{-1}{4}$
$x_1=\dfrac{8}{45}$ et $x_2=\dfrac{5}{-4}$
$x_1=\dfrac{-4}{9}$ et $x_2=\dfrac{3}{2}$
$P(x)$ n'a pas de racines
Question 7
Trouver les racines de $P(x)=12x^2-9x-3$. On cherchera une racine évidente.
$x_1=\dfrac{1}{2}$ et $x_2=\dfrac{-1}{4}$
$x_1=1$ et $x_2=\dfrac{-1}{4}$
$x_1=\dfrac{1}{2}$ et $x_2=\dfrac{1}{4}$
$x_1=1$ et $x_2=\dfrac{1}{4}$
Question 8
Trouver les racines de $P(x)=18x^2+11x-4$.
$x_1=\dfrac{-11-\sqrt{409}}{36}$ et $x_2=\dfrac{-11+\sqrt{409}}{36}$
$x_1=\dfrac{11-\sqrt{409}}{36}$ et $x_2=\dfrac{11+\sqrt{409}}{36}$
$x_1=\dfrac{11+\sqrt{409}}{36}$ et $x_2=\dfrac{11+\sqrt{409}}{36}$
$x_1=\dfrac{-11-\sqrt{18}}{36}$ et $x_2=\dfrac{-11+\sqrt{18}}{36}$
Question 9
Trouver les racines de $P(x)=-x^2-3x+\dfrac {1}{4}$.
$x_1=\dfrac{-1-\sqrt{8}}{-2}$ et $x_2=\dfrac{-1+\sqrt{8}}{-2}$
$x_1=\dfrac{3-\sqrt{10}}{-2}$ et $x_2=\dfrac{3+\sqrt{10}}{-2}$
$x_1=\dfrac{-1-\sqrt{10}}{2}$ et $x_2=\dfrac{-1+\sqrt{10}}{2}$
$x_1=\dfrac{2-\sqrt{8}}{2}$ et $x_2=\dfrac{2+\sqrt{8}}{2}$
Question 10
Trouver les racines de $P(x)=2x^2-x-1$. On cherchera une racine évidente.
$x_1=1$ et $x_2=2$
$x_1=\dfrac{1-\sqrt{9}}{-4}$ et $x_2=\dfrac{1+\sqrt{9}}{-4}$
$x_1=\dfrac{-1}{2}$ et $x_2=1$
$x_1=-1$ et $x_2=10$
