Fiche de cours
Centre de gravité d'un triangle
Rappel : milieu d'un segment
Soient $B$ et $C$ deux points du plan,
$A'$ est le milieu de $[BC]$ si et seulement si $\overrightarrow{BA'} = \dfrac{1}{2} \overrightarrow{BC}$ ce qui est équivalent à dire en utilisant la relation de Chasles que $\overrightarrow{A'B} + \overrightarrow{A'C}= \overrightarrow{0}$
Définition :
Soit $ABC$ un triangle, il existe un point du plan, noté $G$, et un seul, tel que
$\overrightarrow{GA} + \overrightarrow{GB} + \overrightarrow{GC} = \overrightarrow{0}$.
Ce point est appelé le centre de gravité du triangle.
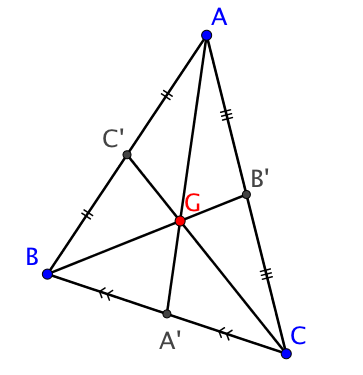
1. Point de concours des médianes
On réécrit cette égalité en faisant apparaitre le point $A$ dans les deux derniers vecteurs par la relation de Chasles.
Cela devient alors
$\overrightarrow{GA} + (\overrightarrow{GA} + \overrightarrow{AB}) + (\overrightarrow{GA} + \overrightarrow{AC}) = \overrightarrow{0}$
En regroupant les $\overrightar
