1) Dériver chacune des fonctions suivantes.
a) $\forall x \in \mathbb{R}$, $f(x) = (1+x)(x^2 + 3x+1)$
b) $\forall x \in \mathbb{R} +\ast$, $f(x) = x\sqrt{x}$
c) $\forall x \in \mathbb{R} \backslash{1}$, $f(x) = \dfrac{3x^2 + 2x -1}{1-x}$
2) Calculer la dérivée de la fonction suivante, déduire son tableau de variation et préciser ses extremums.
$\forall x \in \mathbb{R}$, $f(x) = x^3 + x^2 - x+2$
1) a) La fonction $f$ est dérivable sur $\mathbb{R}$ en tant que produit de fonctions dérivables (polynômes) sur $\mathbb{R}$
On remarque que $f=uv$, avec $\forall x \in \mathbb{R}$, $u(x) =1+x$ et $v(x) = x^2 +3x+1$.
On en déduit : $f'=u'v+uv'$
Sachant que : $\forall x \in \mathbb{R}$, $u'(x) = 1$ et $v'(x) = 2x+3$
On en conclut :
$\forall x \in \mathbb{R}$, $f'(x) = 1 \times (x^2+3x +1) + (1+x)(2x+3)$
$\forall x \in \mathbb{R}$, $f'(x)= x^2 +3x+1+2x+3+2x^2+3x$
$\forall x \in \mathbb{R}$, $f'(x)= 3 x^2+8x +4$
b) La fonction $f$ est dérivable sur $\mathbb{R}+ \ast$ en tant que produit de fonctions dérivables sur $\mathbb{R}+ ast$.
On remarque que $f=uv$, avec $\forall x \in \mathbb{R}+\ast$, $u(x) = x$ et $v(x) = \sqrt{x}$.
On en déduit : $f'=u'v +uv'$
Sachant que $\forall x \in \mathbb{R}+\ast$, $u'(x) = 1$ et $v'(x) = \dfrac{1}{2 \sqrt{x}}$
$\forall x \in \mathbb{R}+ \ast$,
$f'(x) = 1\times \sqrt{x} + x \times \dfrac{1}{2\sqrt{x}} $
$f'(x)= \sqrt{x} + \dfrac{\sqrt{x} \times sqrt{x}}{2\sqrt{x}} = \sqrt{x} + \dfrac{\sqrt{x}}{2}$
On en conclut :
$\forall x \in \mathbb{R}+\ast$, $f'(x) = \dfrac{3\sqrt{x}}{2}$
c) La fonction $f$ est dérivable sur $\mathbb{R} \backslash{1 }$ en tant que quotient de fonctions dérivables sur $\mathbb{R} \backslash{1 }$, dont le dénominateur ne s'annule pas.
On remarque que $f=\dfrac{u}{v'}$, avec $\forall x \in \mathbb{R} \backslash{1}$, $u(x) = 3x^2 + 2x-1$ et $v(x)=1-x$.
On en déduit que $f'= \dfrac{u'v-uv'}{v^2}$
Sachant que : $\forall \in\mathbb{R}\backslash{1}$, $u'(x) = 6x+2$ et $v'(x)=-1$
On en conclut :
$f'(x) = \dfrac {(6x+2)(1-x)-(3x^2+2x-1) \times (-1)}{(1-x)^2}$
$f'(x) = \dfrac{-3x^2 + 6x +1}{(1-x)^2}$
2) Calcul de la dérivée.
La fonction $f$ est dérivable sur $mathbb{R}$ en tant que polynôme.
$\forall x \in \mathbb{R}$, $f'(x) = 3x^2 + 2x-1$
Etude du signe de la dérivée.
On remarque que $f'(x)$ est un trinôme du second degré. On calcule donc son discriminant pour étudier son signe :
$\Delta = b^2 - 4ac = 2^2 - 4 \times 3 \times (-1) = 16$
Sachant que $\Delta>0$, on en déduit que le trinôme admet deux racines $x1$ et $x2$, et est du signe de $a$, c'est-à-dire positif ($a=3$), à l'extérieur des racines, et du signe contraire entre ses racines :
$x_1 = \dfrac{-b - \sqrt{\Delta}}{2a} = \dfrac{-2-4}{6} = -1$
$x_2 = \dfrac{-b + \sqrt{\Delta}}{2a} = \dfrac{-2+4}{6} = \dfrac{1}{3}$
Variations.
Sachant que $f$ est décroissante lorsque $f'(x) \le 0$ et croissante lorsque $f'(x) \ge 0$, on en déduit que :
$f$ est croissante sur $]- \infty, -1] \bigcup [\dfrac{1}{3}; +\infty[$
$f$ est décroissante sur $[-1; \dfrac{1}{3}]$.
Calcul des extremums.
La dérivée s'annulant et changeant de signe en $-1$ et $\dfrac{1}{3}$, on en déduit que $f$ admet des extremums locaux en ces points :
$f(-1) = 3$
$f \left( {\dfrac{1}{3}} \right) = \dfrac {49}{27}$
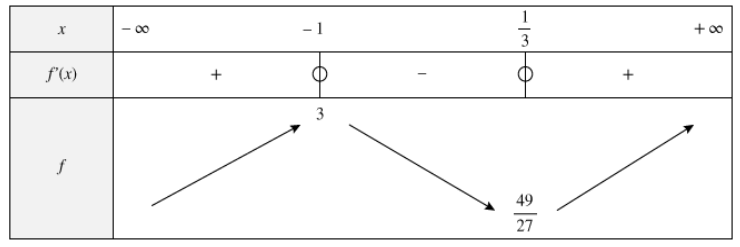
Construction du tableau de variation.
On peut enfin dresser le tableau de variation de $f$ :