L'énoncé
Cet exercice est un QCM. Cocher la ou les bonnes réponses.
Tu as obtenu le score de
Question 1
La fonction \(f\) définie par \(f(x) = \dfrac{1}{2x^2+1} \) :
A pour ensemble de définition \(\mathbb{R}\backslash \{-\frac{1}{2} \}\).
A pour ensemble de définition \(\mathbb{R}\).
Est décroissante sur \(] - \infty;0]\).
Admet un maximum sur \(\mathscr{D_f}\).
\(f\) est définie \(\Leftrightarrow 2x^2 + 1\neq 0\)
Utilise ensuite les fonctions associées pour trouver les variations de \(f\).
\(f\) est définie \(\Leftrightarrow 2x^2 + 1\neq 0\)
Mais \(2x^2 + 1 =0 \Leftrightarrow x^2 = -\large \frac{1}{2} \) ce qui est impossible sur \(\mathbb{R}\).
\(x \longmapsto x^2 \) est décroissante sur \(] -\infty;0] \) donc \(x \longmapsto 2x^2 +1 \) aussi et donc \(f\) est croissante.
\(x \longmapsto x^2 \) est croissante sur \([ 0 ; + \infty[\) donc \(x \longmapsto 2x^2 +1 \) aussi et donc \(f\) est décroissante.
\(f\) admet donc un maximum sur \(\mathscr{D_f}\) pour \(x=0\).
Question 2
La fonction \(f\) définie sur \(\mathscr{D_f}\ = [ -5 ; +\infty[ \) définie par \( f(x) = -2\sqrt{x+5}\) est :
Croissante sur \([-5;+\infty[\).
Décroissante sur \([-25,+\infty[\).
Croissante sur \([0,+\infty[\).
Décroissante sur \([-5;+\infty[\).
\(x \longmapsto x+5 \) est une fonction affine.
Utilise ensuite les fonctions associées pour trouver les variations de \(f\).
Sur \(\mathscr{D_f}= [-5 ; +\infty[ \):
\(x \longmapsto x+5 \) est croissante (fonction affine) donc \(x \longmapsto \sqrt{ x+5} \) aussi et en multipliant par \(-2\) , \(f\) est donc décroissante .
Question 3
Soit \(u\) une fonction croissante sur un intervalle \(I\) et strictement positive sur \(I\). Quelles fonctions ont les mêmes variations que \(u\) sur \(I\) ?
\(- 2u + 3\)
\( 4 + \dfrac{2}{u}\)
\(-5 \sqrt{u}-7 \)
\(\dfrac{-3}{2\sqrt u }\)
Quelles sont les variations de \(u\) sur \(I\) ?
Utiliser ensuite les fonctions associées pour trouver les variations des fonctions proposées.
Sur \(I\) : \(u\) est croissante donc \(-2u\) est décroissante et \(-2u+3\) aussi.
Sur \(I\) : \(u\) est croissante donc \(\frac{2}{u}\) est décroissante et \(4+\frac{2}{u}\) aussi.
Sur \(I\) : \(u\) est croissante donc \(\sqrt u \) est décroissante et \(-5\sqrt u-7\) est décroissante.
Sur \(I\) : \(u\) est croissante et positive donc \(2\sqrt u \) est croissante. Comme \(u\) est non nulle \(\large \frac{3}{2\sqrt{u}}\) est décroissante et donc \(-\large \frac{3}{2\sqrt{u}}\) est croissante.
Question 4
Soit \(u\) une fonction dont on donne ci-dessous le tableau de variations sur \(\mathscr{D_u}=[2 ; 8]\).
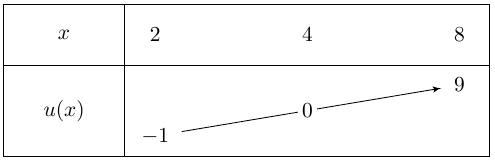
Quels sont les tableaux de variations corrects parmi ceux proposés ?
Utilise ensuite les fonctions associées pour trouver les variations des fonctions proposées. \(\dfrac{1}{u}\) est définie pour \( u\) non nulle.
\(\sqrt u \) est définie pour \( u\) positive.
Pense à vérifier les valeurs des images.
\(u \) est croissante sur \(\mathscr{D_u}\)donc \(u -3\) aussi. Proposition 1 fausse.
\(u \) est croissante sur \(\mathscr{D_u}\) donc \(5u \) aussi, mais \(5u \) est définie aussi sur \(\mathscr{D_u}\) pas sur \([10 ; 40] \). Proposition 2 fausse.
\(\large \frac{1}{u} \) est définie pour \(u\) non nulle donc sur \( I = [2 ; 4[ \bigcup ]4 ; 8] \)
\((u)\) est croissante sur \(\mathscr{D_u}\) donc \(\large \frac{1}{u} \) est décroissante sur \([2 ; 4[ \) et sur \(]4 ; 8]\)
\(u(2) = - 1\) donc \(\large \frac{1}{u(2)} = \frac{1}{-1} \normalsize = - 1 \) et \(u(8) = 9\) donc \(\large \frac{1}{u(8)} = \frac{1}{9} \). Proposition 3 correcte.
\(\sqrt u \) est définie pour \(u)\) positive donc sur \( I =[4 ; 8] \)
\((u)\) est croissante sur \( I =[4 ; 8]\) donc \(\sqrt u \) aussi.
\(u(4) = 0\) donc \(\sqrt u(4) = \sqrt 0 =0 \) et \(u(8) = 9\) donc \(\sqrt u(8) = \sqrt{9} = 3 \). Proposition 4 f
Question 5
La fonction \(f\) définie par \(f(x) = \dfrac{3}{-x^2 + 2x + 15}\) :
Est définie sur \(\mathscr{D_f} = ]-3 ; 5[\).
Est définie sur \(\mathscr{D_f} = [-3 ; 5] \).
Admet un maximum sur \(\mathscr{D_f}\).
Admet un minimum sur \(\mathscr{D_f}\).
\(-x^2 + 2x + 15\) est un polynôme; quel est son signe ?
Utilise ensuite les fonctions associées pour trouver les variations de \(f\) et chercher si elle admet un maximum ou un minimum.
A quelle(s) condition(s) \(f\) est-elle définie ?
\(f\) est définie \(-x^2 + 2x + 15 \geq 0\) et \(\sqrt{-x^2 + 2x + 15} \neq 0\) donc pour \(-x^2 + 2x + 15 > 0\)
\( -x^2 + 2x + 15 \) est un polynôme dont le discriminant est \(\Delta = 64\) et qui admet deux racines : \(- 3\) et \(5\).
Il est positif (donc du signe opposé de \(a = - 1\)) entre ses racines donc sur \([- 3 ; 5]\) donc strictement positif sur \(\mathscr{D_f}=]-3 ; 5[\)
Sur \(\mathscr{D_f}\) :
\(x \longmapsto -x^2 + 2x + 15 \) est croissante sur \(] – 3 ; 1]\) et décroissante sur \([1 ; 5[\) donc :
\(x \longmapsto \sqrt{-x^2 + 2x + 15} \) aussi.
\(x \longmapsto \large\frac{3}{\sqrt{-x^2 + 2x + 15}} \) est décroissante sur \(] – 3 ; 1]\) et croissante sur\( [1 ; 5[\) donc \( f\) admet un minimum sur \(\mathscr{D_f}\).




