Fiche de cours
Variations des fonctions associées
Soit $u$ un fonction définie sur $I$, on s'intéresse aux variations de la fonction obtenue après transformation (addition, multiplication ...).
1) la fonction $u + k, \ k \in \mathbb{R}$.
La fonction $u + k$ a les mêmes variations que la fonction $u$.
Par exemple la fonction $x^2 + 3$ a les mêmes variations que la fonction $x^2$ : elle est décroissante pour $x$ négatif et croissante pour $x$ positif.
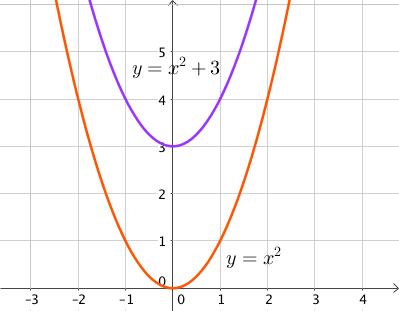
Ainsi, ajouter $k$ à une fonction $u$ revient à translater la courbe de la fonction $u$ de $k$ unités selon l'axe des ordonnées.
2) la fonction $\lambda u, \ \lambda \in \mathbb{R}$
Si $\lambda < 0$, les variations de $\lambda u$ sont contraires à celles de $u$.
Si $\lambda > 0$, les variations de $\lambda u$ sont identiques à celles de $u$.
Par exemple, la fonction $\sqrt{x}$ est croissante sur $\mathbb{R}^+$. Ainsi, la fonction $-2\sqrt{x}$ est décrois
