L'énoncé
Soit la fonction définie sur $\mathbb{R}$ par
$f(x) = 2x^2 - 3x -5$
Question 1
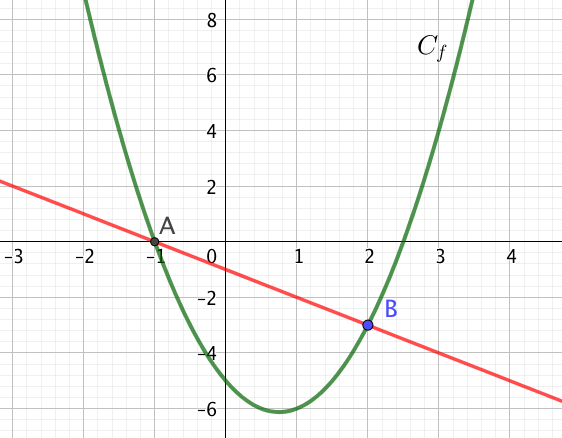
Tracer la courbe représentative $(C)$ dans un repère orthonormal (unités = 1 cm).

Question 2
Trouver les nombres $a$ et $b$ tels que $f(x) = 2 [ (x-a)^2 +b ]$
On développe :
$f(x) = 2 \left [ (x-a)^2 +b \right ] = 2 \left [x^2 - 2ax + a^2 + b \right ] = 2x^2 - 4ax + 2a^2 + 2b$
En identifiant les coefficients, on a :
$\left \{ \begin{array}{ll} -4a = -3 \\ 2a^2 + 2b = -5 \end{array} \right. \Leftrightarrow \left \{ \begin{array}{ll} a = \dfrac{3}{4} \\ 2b = -5-2 \left( \dfrac{9}{16} \right) = \dfrac{ -49}{8} \end{array} \right. \Leftrightarrow \left \{ \begin{array}{ll} a = \dfrac{3}{4} \\ b = \dfrac{-49}{16} \end{array} \right.$
D'où :
$f(x) = 2 \left [ \left(x- \dfrac{3}{4} \right) ^2 - \dfrac{49}{16} \right ]$
Question 3
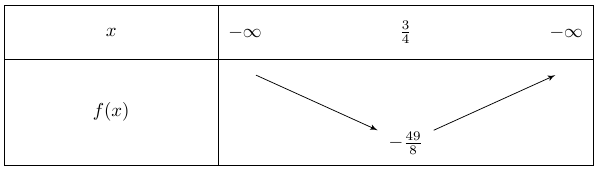
Étudier les variations de $f$ et dresser son tableau de variations.
Les variations dépendent en fait du terme $\left( x - \dfrac{3}{4} \right)^2$ qui change de sens de variation suivant que $x < \dfrac{3}{4}$ (décroissant) ou $x > \dfrac{3}{4}$ (croissant).
Lorsqu'on soustrait $\dfrac{49}{16}$ ça ne change rien et lorsqu'on multiplie par $2$ non plus.
On vérifie que $f\left(\dfrac{3}{4}\right)=-\dfrac{49}{8}$
Question 4
Résoudre par le calcul l'équation $f(x) = 0$
$f(x) = 0 \Leftrightarrow 2 \left [ \left(x- \dfrac{3}{4} \right) ^2 - \dfrac{49}{16} \right] = 0$
$\Leftrightarrow 2 \left[ \left( x- \dfrac{3}{4} - \dfrac{7}{4} \right) \left( x - \dfrac{3}{4} + \dfrac{7}{4} \right) \right] = 0$
$ \Leftrightarrow \left( x - \dfrac{5}{2} \right) \left( x + 1 \right) = 0$
On retrouve bien les solutions $-1$ et $\dfrac{5}{2}$
Question 5
Tracer sur la même figure la droite $(AB)$ où $A$ a pour coordonnées $(-1; 0)$ et $B(2; -3)$
Question 6
Déterminer l'équation de la droite $(AB)$
On cherche une équation de la forme $y=ax+b$
Calculons de coefficient directeur de $(AB)$ :
$a=\dfrac{y_B-y_A}{x_B-x_A}$
$a=\dfrac{2+1}{-3+0}$
$a=-1$
$A$ appartient à la droite d'équation $y=-x+b$ donc en remplaçant ses coordonnées on trouve :
$0=1+b$ soit $b=-1$
Finalement : $(AB)$ : $y = - x -1$
Question 7
Quelle inéquation doit-on résoudre si l'on veut déterminer les valeurs de $x$ pour lesquelles ($C$) est au-dessus de ($AB$) ?
La résolution n'est pas obligatoire.
Il faut résoudre $f(x) > -x -1$ ; les solutions sont ici :
$x \in ] - \infty \ ; \ -1 ] \cup [2 \ ; \ + \infty [$
