Fiche de cours
Nombre dérivé
Définition :
Soient $f$ une fonction définie sur $I$ et $a$ et $b$ deux points appartenant à la courbe représentative de la fonction $f$ ayant pour coordonnées respectives $(a; f(a))$ et $(a+h; f(a+h))$ où $h$ est un réel,
le coefficient directeur de la droite $(AB)$ est $\dfrac{y_B - y_A}{x_B - x_A} = \dfrac{f(a+h) - f(a)}{a + h - a} = \dfrac{f(a+h) - f(a)}{h}$ : c'est aussi le taux d'accroissement.
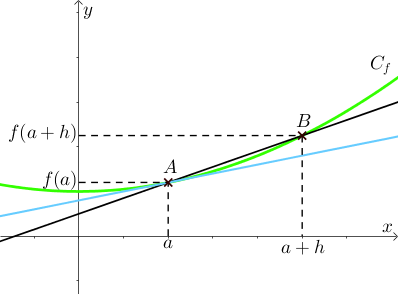
Le réel $h$ est choisi de plus en plus petit de telle manière que le point $B$ se rapproche du point $A$ et que la droite $(AB)$ se rapproche de la droite bleue.
On notera alors $\lim \limits_{h \to 0} \dfrac{f(a+h) - f(a)}{h}$.
Si le résultat de ce calcul est un réel $l$, alors la fonction $f$ est dérivable en $a$ et $l$ est noté $f'(a)$ :
$f'(a)$ est le nombre dérivé de la fonction $f$ au point $a$.
Exemple :
On considère $f
