L'énoncé
Cet exercice est un QCM. Cocher la ou les bonnes réponses.
Tu as obtenu le score de
Question 1
Les solutions sur \(\mathbb{R}\) de l'équation \(|x - 5| = 3\) sont :
$2$
$-2$ et $8$
$2$ et $8$
$-8$
Écrire l'équation sans valeur absolue selon les valeurs de \(x\).
Résoudre alors les deux équations obtenues.
\(x - 5 \geq 0 \Leftrightarrow x \geq 5 \) et \( x – 5 \leq 0 \Leftrightarrow x \leq 5\)
Si \(x \geq 5 \) alors \(|x - 5| = x – 5\) et donc :
\(|x – 5| = 3\Leftrightarrow x – 5 = 3 \Leftrightarrow x = 8\)
Si \(x \leq5\) alors \(|x - 5| = - x + 5\) et donc :
\(|x – 5| = 3 \Leftrightarrow - x + 5 = 3 \Leftrightarrow - x = - 2\Leftrightarrow x = 2\)
Conclusion : l'ensemble des solutions de l'équation est \(S = \{ 2 ; 8 \}\)
Question 2
Les solutions sur \(\mathbb{R}\) de l'équation \(|x - 2| = |x +1|\) sont :
\(\dfrac{1}{2}\)
-\(\dfrac{1}{2}\)
$0$
$1$
Dans un tableau (type tableau de signes) écrire \(|x – 2|\) sans valeur absolue selon les valeurs de \(x\).
De même, écrire \(|x + 1|\) sans valeur absolue selon les valeurs de \(x\).
Résoudre alors les 3 équations possibles.
\(x - 2 \geq 0 \Leftrightarrow x \geq 2 \) et \( x – 2\leq 0 \Leftrightarrow x \leq 2\)
Si \(x \geq 2\) alors \( |x - 2| = x – 2 \) et si \( x \leq 2\) alors \( |x - 2| = - x + 2\)
De même, si \(x \geq - 1\) alors \(|x + 1| = x + 1\) et si \( x\leq - 1\) alors \(|x + 1| = - x – 1\)
On obtient alors le tableau suivant :
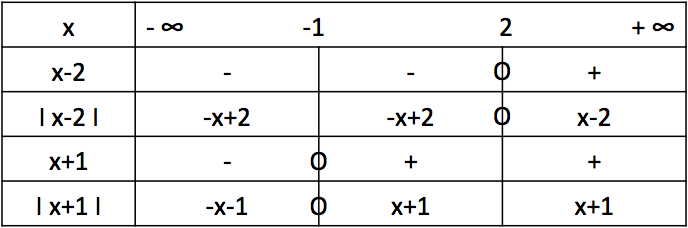
On résout alors les équations sur chacun des 3 intervalles. Attention de bien vérifier que la valeur de \(x\) obtenue appartient bien à l'intervalle choisi !
Pour \(x \in ]-\infty ; - 1], |x – 2| = |x + 1| \Leftrightarrow - x + 2 = - x – 1 \Leftrightarrow 0x +2 = -1\). Impossible donc pas de solutions sur \( ]-\infty ; - 1]\)
Pour \( x \in [-1 ; 2], |x – 2| = |x + 1| \Leftrightarrow - x + 2 = x + 1 \Leftrightarr
Question 3
Soit l'expression \(A(x) = 2 + 5|x - 1| - 3|2 - x|\). Alors :
\(x \leq 1\) on a \(A(x) = - 2x + 1\)
\(x \in [1 ; 2 ]\) on a \(A(x) = 2x – 3\)
\( x \geq 2\) on a \(A(x) = 2x + 3\)
\( x \geq 2\) on a \(A(x) = 8x - 11\)
Dans un tableau (type tableau de signes) écrire \(|x – 1|\) puis \(5|x - 1|\) sans valeur absolue selon les valeurs de \( x \)
De même, écrire \(|2 - x| \) puis \(- 3|2 - x|\) sans valeur absolue selon les valeurs de \(x\).
Donner alors l'expression de \(A(x)\) selon les valeurs de \( x\).
On obtient le tableau suivant :
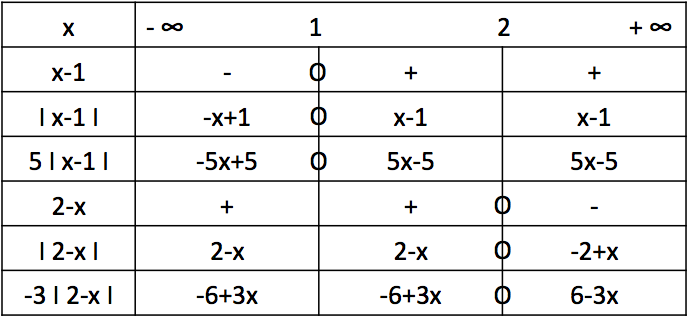
Pour \(x \leq 1\) on a \(A(x) = 2 - 5x + 5 – 6 + 3x\)
\(A(x) = 1 – 2x \) soit \(A(x) = - 2x + 1\)
Proposition 1 vraie.
Pour \(x \in [1 ; 2 ]\) on a \(A(x) = 2 + 5x - 5 – 6 + 3x\)
\(A(x) = – 9 + 8x \) soit \( A(x) = 8x - 9\)
Proposition 2 fausse.
Pour \( x \geq 2\) on a \(A(x) = 2 + 5x - 5 + 6 - 3x\)
\(A(x) = 3 + 2x \) soit \(A(x) = 2x + 3\)
Proposition 3 vraie et 4 fausse.
Question 4
Soit \(f\) la fonction définie sur \(\mathbb{R}\) par \(f(x) = 3|x| - 1\).
\(f\) est croissante sur \([ 0 ; + \infty[\)
\(f\) admet un maximum pour \(x = 0\)
\(f\) est positive sur \([ - 1 ; 1]\)
\(f\) s'annule en \(-\dfrac{1}{3}\)
Écrire \(f(x)\) sans valeur absolue.
Étudier la fonction obtenue !
Si \(x \geq 0\) alors \(f(x) = 3x - 1\) et donc sur \([0 ; +\infty[ f\) est croissante.
Si \(x \leq0 \) alors \( f(x) = 3( - x) - 1\) soit \(f(x) = - 3x - 1\) et donc sur \(] –\infty ; 0]\; f \) est décroissante.
Ainsi \(f\) admet un minimum en \(0\) et non pas un maximum.
Comme \(f\) est croissante sur \([0 ; +\infty[\) et s'annule en \(-\dfrac{1}{3}\)alors \(f\) ne peut pas être positive sur \(-1;1]\).
Faire un tableau de variation pour visualiser ce résultat au besoin.
\(f(-\frac{1}{3}) = 3|-\frac{1}{3}| - 1 = 3 \frac{1}{3} - 1 = 0\)
Question 5
L'ensemble des solutions sur \(\mathbb{R}\) de l'inéquation \(|3- x|\leq 2\) est :
\(S = [1 ; 5]\)
\(S = ] – \infty ; 5]\)
\(S = [1 ; +\infty[\)
Aucune solution.
Résoudre les deux inéquations obtenues.
Écrire \(|3 – x| \) sans valeur absolue.
\(3 - x \geq 0 \Leftrightarrow x \leq 3\) et \( 3 - x\leq 0 \Leftrightarrow x \geq 3\)
Si \(x \geq 3\) alors \(|3 - x| = - 3 + x \) et donc :
\(|3 - x| \leq 2 \Leftrightarrow - 3 + x \leq 2 \Leftrightarrow x \geq 5\)
Les nombres cherchés doivent donc vérifier deux conditions : \(x \geq3 \) et \(x \leq 5\). Ainsi \( S_1 = [3 ; 5]\)
Si \(x \leq 3 \) alors\( |3 - x| = 3 - x\) et donc :
\(|3 - x| \leq 2\Leftrightarrow 3 - x \leq 2\Leftrightarrow x \geq 1\)
Les nombres cherchés doivent donc vérifier deux conditions : \(x \leq3 \) et \(x \geq 1\). Ainsi \( S_2 = [1 ;3]\)
Conclusion : l'ensemble des solutions de l'inéquation est la réunion des deux intervalles soit \( S = [3 ; 5] \cup [1 ; 3] \)
Conclusion : \(S = [1 ; 5]\).
