Une mine produit $x$ kg d’un minerai par jour, $x \in [0;10]$ ($x$ varie selon les jours), le coût total d’extraction de ces $x$ kg est donné par :
$C(x) = x^3$ où C est en euros.
Chaque kg est vendu $81$ euros, soit pour $x$ kg vendus, une recette de $R(x) = 81 \times x$ euros.
Le bénéfice associé à la fabrication et à la vente de $x$ kg est donné par $B(x) = R(x) − C(x)$.
1) Détailler les calculs de $C(5)$, $R(5)$, $B(5)$ et en déduire si une production de 5 kg est rentable.
2) Justifier si une production de 10 kg est rentable.
3) Compléter le tableau de valeurs puis construire les courbes des fonctions $C$ et $R$ dans le repère donné.
| $x$ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| $C(x)=x^3$ | |||||||||||
| $R(x)=81x$ |
4) Déterminer graphiquement et algébriquement à $0,1$ kg près, la production qui assure une recette de $400$ euros, en déduire le bénéfice réalisé à l’euro près.
5) Déterminer graphiquement et algébriquement à $0,1$ kg près, la production qui assure un coût d’au moins $500$ euros.
6) Déterminer graphiquement l’intervalle des productions qui assurent un bénéfice positif. Montrer que $B(x) = x(9 − x)(9 + x)$ et retrouver algébriquement l’intervalle précédent.
7) Déterminer graphiquement la production qui assure un bénéfice maximal.
8) Recopier et compléter le tableau de valeurs suivant puis construire la courbe de $B$ dans le repère précédent.
| $x$ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| $B(x)$ |
Construire les tableaux de signes et de variations puis les extremums de $B$ pour $x \in [0;10]$
(Estimer la production optimale à la calculatrice à 0,1 près.)
9) Ces résultats sont-ils cohérents avec les résultats des questions 6 et 7 ?
10) Calculer le bénéfice mensuel (30 jours) pour la production optimale.
1) $C(5) = 5^3 = 125$ euros
$R(5) = 81 \times 5 = 405$ euros
$B(5) = R(5) - C(5) = 405 - 125$ = 280 euros
Donc une production de $5$ kg est rentable car la recette est supérieure au coût ($405$ > $125$) ou bien car le bénéfice est positif ($280$ > $0$).
2) $C(10) = 10^3 = 1000$ euros
$R(10) = 81 \times 10 = 810$ euros
$B(10) = R(10) - C(10) = 810 - 1000 = - 190$ euros
Donc une production de $10$ kg n’est pas rentable car la recette est inférieure au coût ($810$ < $1000$)
Ou bien car le bénéfice est négatif ($−190$ < $0$).
3) Tableau de valeurs et courbes des fonctions $C$ et $R$ dans le repère donné :
| $x$ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| $C(x) = x^3$ | 0 | 1 | 8 | 27 | 64 | 125 | 216 | 343 | 512 | 729 | 1000 |
| $R(x) = 81 x$ | 0 | 405 | 810 |
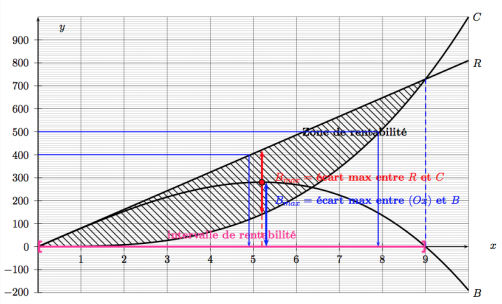
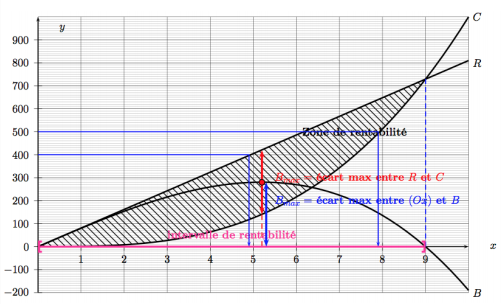
4) Graphiquement : $R(x) = 400$ lorsque $x \approx 5$
Algébriquement : $R(x) = 400$, équivaut à $81x = 400$, soit : $x= \frac{400}{81} \approx 4,9$
Ainsi la recette vaut $400$ euros pour $x \approx 4,9 kg$.
$B(4,9) = R(4,9) - C(4,9) = 400 - 4,9^3 \approx 282$
Soit $282$ euros de bénéfice réalisé à l'euro près.
5) Graphiquement : $C(x)$ > $500$ lorsque $x$ > $7,9$.
Algébriquement : $C(x)$ > $500$ équivaut à $x^3$ > $500$
Soit $x$ > $\sqrt[3]{80} \approx 7,9$, donc le coût vaut au moins $500$ euros pour $x$ > $7,9$ kg.
6) Graphiquement : le bénéfice est strictement positif si la recette est strictement supérieure au coût.
Soit : $B(x)$ > $0$ lorsque $R(x)$ > $C(x)$ ; c'est à dire lorsque $x \in ]0;9[$.
L'intervalle de rentabilité des productions qui assurent un bénéfice positif est donc ]0;9[.
Algébriquement : $B(x) = R(x) - C(x) = 81x - x^3 = x(81-x^2) = x(9^2-x^2) = x(9-x)(9+x)$.
Il suffit d'étudier le signe de $x(9-x)(9+x)$ dans un tableau de signes pour $x \in [0;10]$.
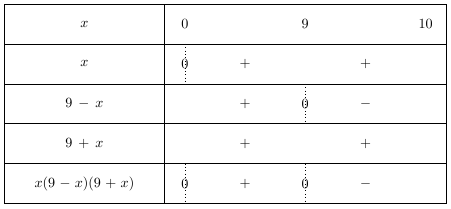
Conclusion : $B(x) > 0$ lorsque $x \in ]0;9[$ (cohérent avec le résultat graphique).
7) Graphiquement la production qui assure un bénéfice maximal est $x \approx 5.2$
En effet, en ce point, l'écart est maximal entre les courbes de $R$ et $C$ dans l'intervalle de rentabilité.
8) La courbe de B est construite dans le repère ci-dessus.
| $x$ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| $B(x) = 81x - x^3$ | 0 | 80 | 154 | 216 | 260 | 280 | 270 | 224 | 136 | 0 | -190 |

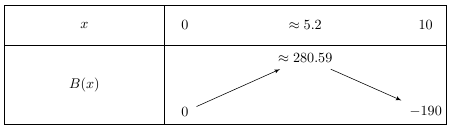
9) Extremums de B(x) pour $x \in [0;10]$ : le minimum vaut $-190$ pour $x=10$ et le maximum vaut $\approx 280.59$ pour $x \approx 5.2$.
En effet, la calculatrice donne :
| $x$ | 5.1 | 5.2 | 5.3 |
| $B(x)$ | 280.45 | 280.59 | 280.42 |
Ces résultats sont cohérents avec les résultats des questions précédentes.
10) Le bénéfice mensuel (30 jours) pour la production optimale est : $B_m = 280,59 \times 30 = 8417,7$ euros.
