L'énoncé
Cet exercice est un QCM. Cocher la ou les bonnes réponses.
Tu as obtenu le score de
Question 1
Soit \(f\) la fonction définie par \(f(x) = (- x)^3\). Quelles sont les propositions correctes ?
\(f\) est définie sur \(\mathbb{R}\backslash \{0 \}\)
\(f\) est décroissante sur son ensemble de définition.
\(f(-5) = 125\)
\(f(-5) = -125\)
Quel est l'ensemble de définition de la fonction cube ?
A quelle condition l'expression (\(-x)\) est-elle définie ?
Calculez l'image de \(– 5\) !
La fonction cube est positive sur \([ 0 ; + \infty[\)et négative sur \(]-\infty ; 0]\)
Soient \(a\) et \(b\) deux réels tels que \(a < b\) alors :
\(-a > -b\) soit \(-b>-a \)
La fonction cube étant croissante sur \(\mathbb{R}\) on en déduit que : \((- b)^3 < (- a)^3\).
On a donc \(f(b) < f(a)\).
En conclusion : pour \(a\) et \(b\) réels tels que \(a < b\) on a \(f(b) < f(a)\) et \(f\) est décroissante sur \(\mathbb{R}\).
\(f\) est définie sur sur \(\mathbb{R}\).
\(f( - 5) = ( - ( -5))^3 = (5)^3 = 125\)
Question 2
On désigne par \(f\) la fonction cube et \(g\) la fonction carré. Soit $f(x)=x^3$ et $g(x)=x^2$
\(\mathscr{C_f}\) est au-dessus de \(\mathscr{C_g}\) sur \([1;+ \infty[\)
\(\mathscr{C_f}\) est au-dessous de \(\mathscr{C_g}\) sur \(\mathbb{R}\)
\(\mathscr{C_f}\) est au-dessous de \(\mathscr{C_g}\) sur \(]- \infty;0]\)
\(\mathscr{C_f}\) est au-dessous de \(\mathscr{C_g}\)
Que vaut \(f(x)\) ? et \(g(x)\) ?
Quelle technique utilise-t-on pour déterminer la position relative de deux courbes ?
Attention : le signe d'une différence est souvent difficile à trouver ; factoriser l'expression obtenue.
Calculer \(f(x) – g(x)\) puis chercher son signe sur \(\mathbb{R}\).
Pour \(x \in \mathbb{R}, f(x) – g(x) = x^3 – x^2 \)
Ainsi : \( f(x) – g(x) = x^2(x – 1)\)
\(x^2 \geq0\) sur \(\mathbb{R}\) donc \(f(x) – g(x)\) a le même signe que \(x - 1\)
Si \(x \geq 1\) alors \(x – 1 \geq0\) et
\(f(x) – g(x)\geq0\) soit \( f(x) \geq g(x)\)
Finalement : \(\mathscr{C_f}\) est au-dessus de \(\mathscr{C_g}\)
Ainsi, \(\mathscr{C_f}\) est au-dessus de \(\mathscr{C_g}\) sur \([1 ; +\infty[\)
Si \(x < 1\) alors \(x – 1 <0\) et
\( f(x) – g(x) < 0\) soit \( f(x) < g(x)\)
Ainsi :
\(\mathscr{C_f}\) est au-dessous de \(\mathscr{C_g}\) sur \(]- \infty;0]\)
Vous pouvez bien évidement dresser un tableau de signes si cela vous paraît plus clair.
Question 3
Sachant que \( x\) appartient à \([ - 5 ; 2]\), à quel intervalle appartient \( -2 x^3 + 1 \)?
\([ - 15 ; 251 ]\)
\([ - 251 ; 15 ]\)
\([ - 11 ; 31 ]\)
\([ - 31 ; 11 ]\)
On \(a : – 5 \leq x \leq 2\)
Encadrer alors \(x^3\).
Puis \( – 2x^3\) etc.
On \(a : – 5 \leq x \leq 2\) donc
\((– 5)^3\leq x^3 \leq 2^3\) car la fonction cube est croissante sur \(\mathbb{R}\).
Soit \(- 125 \leq x^3\leq 8\)
D'où, \( 250 \geq -2x^3 \geq - 16 \) (attention : \( - 2 <0\)) ou encore \(-16 \leq -2x^3 \leq 250\)
Ainsi, \(-15 \leq -2x^3 + 1 \leq 251\)
Question 4
La fonction \(g\) définie sur \(\mathbb{R}\) par \(g(x) = -2 x^3 + 1 \)
Est croissante sur \(\mathbb{R}\).
Est décroissante sur \(\mathbb{R}\).
Est croissante sur \([1 ; +\infty[ \).
Admet un maximum sur \(\mathbb{R}\).
Prendre deux réels \(a\) et \(b\) et comparer \(g(a)\) puis \(g(b)\).
On peut aussi utiliser les variations des fonctions associées.
Soient \(a\) et \(b\) deux réels tels que \(a < b\) alors :
\(a^3 < b^3 \) car la fonction cube est croissante sur \(\mathbb{R}\).
Donc, \(-2\times a^3 > -2\times b^3\) (attention :\(-2 < 0) \) ou encore \(-2\times b^3 < -2\times a^3 \)
Et, \(-2\times b^3 +1 < -2\times a^3 + 1\) soit \( g(b) < g(a)\).
En conclusion : pour \(a\) et \(b\) réels tels que \(a < b\) on a \(g(b) < g(a)\) et \(g\) est décroissante sur \(\mathbb{R}\).
Question 5
Soit la fonction \(A\) définie sur \(\mathbb{R}\) par \(A(x) = - 2x^3 + 2x\)
\(A(x)\) s'annule donc trois fois sur \(\mathbb{R}\).
\(A(x) < 0\) sur \(\mathbb{R}\).
\(A(x) \leq 0\) sur \( [-1 ; 0] \cup [1 ; +\infty[ \)
\(A(x) \geq 0 \) sur \( [0 ; 1] \)
Pour trouver le signe d'une expression il est préférable qu'elle soit sous forme de produit ou de quotient.
Factoriser \(A(x)\) sachant que \(x^2 – 1 \) est une identité remarquable, puis chercher le signe à l'aide d'un tableau de signes.
Attention au signe de \((– 2x)\).
Pour \( x \in \mathbb{R}, A(x) = -2x(x^2 – 1)\) soit :
\(A(x) = -2x(x – 1)(x + 1) \)
On obtient alors le tableau de signes suivant :
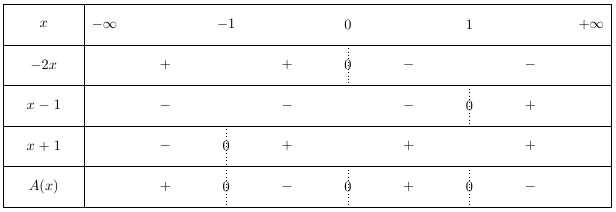
\(A(x)\) s'annule donc trois fois sur \(\mathbb{R}\).
\(A(x) \leq 0\) sur \( [-1 ; 0] \cup [1 ; +\infty[ \) et \(A(x) \geq 0 \) sur \( [0 ; 1] \) mais aussi sur \( ] – \infty ; - 1]\)
