L'énoncé
Le but de l'exercice est de trouver la position de différents nombres relatifs donnés en écriture fractionnaire ou de donner une écriture fractionnaire des nombres relatifs présentés.
Question 1
Soit le point $A(\dfrac{12}{8})$.
Donner une écriture fractionnaire simplifiée de $A$. Puis son écriture décimale. Enfin, placer $A$ sur l'axe des abscisses.
Une écriture fractionnaire simplifiée de $A$ est $A(\dfrac{3}{2})$. En effet, $\dfrac{12}{8} = \dfrac{4 \times 3}{4 \times 2} = \dfrac{3}{2}$. Donc $A(\dfrac{12}{8}) = A(\dfrac{3}{2})$
Par ailleurs, l'écriture décimale de $A$ est $A(1,5)$. En effet, $\dfrac{3}{2} = \dfrac{1,5 \times 2}{1 \times 2} = 1,5$.
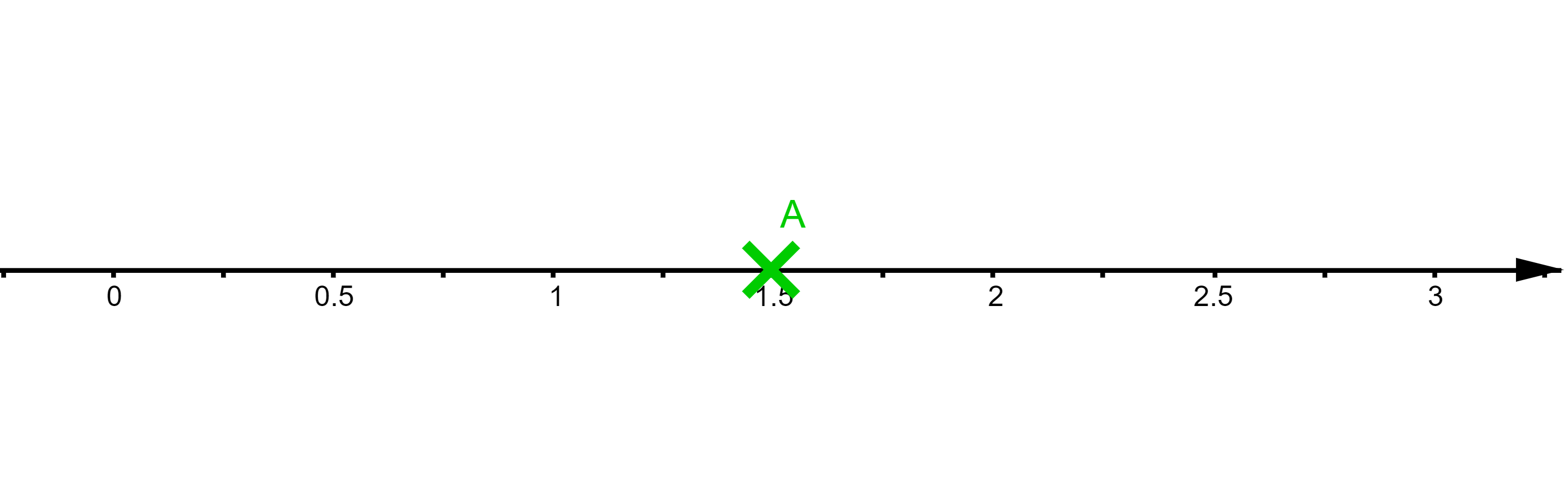
Donc le point $A$ est positionné ainsi sur l'axe des abscisses :
Question 2
Soit le point $B(-\dfrac{21}{60})$
Donner une écriture fractionnaire simplifiée de $B$, puis son écriture décimale, puis placer le point $B$ sur la droite graduée.
L'écriture fractionnaire simplifiée de $B$ est $B(-\dfrac{7}{20})$. En effet, $-\dfrac{21}{60} = -\dfrac{7 \times 3}{20 \times 3} = -\dfrac{7}{20}$
Par ailleurs, son écriture décimale est $B(-0,35)$. En effet, $-\dfrac{7}{20} = -\dfrac{3,5 \times 2}{10 \times 2} = -\dfrac{3,5}{10} = -0,35$
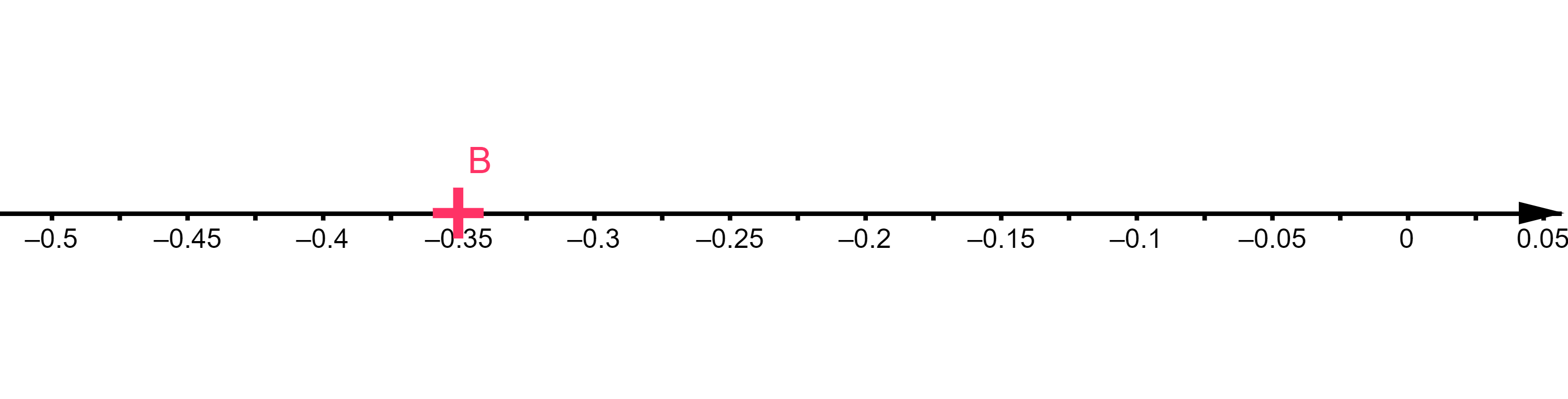
Donc la position de $B$ sur la droite est la suivante :
Question 3
Soit le point $C$ représenté ci-dessous.
Donner son écriture décimale, puis son écriture fractionnaire la plus simplifiée. 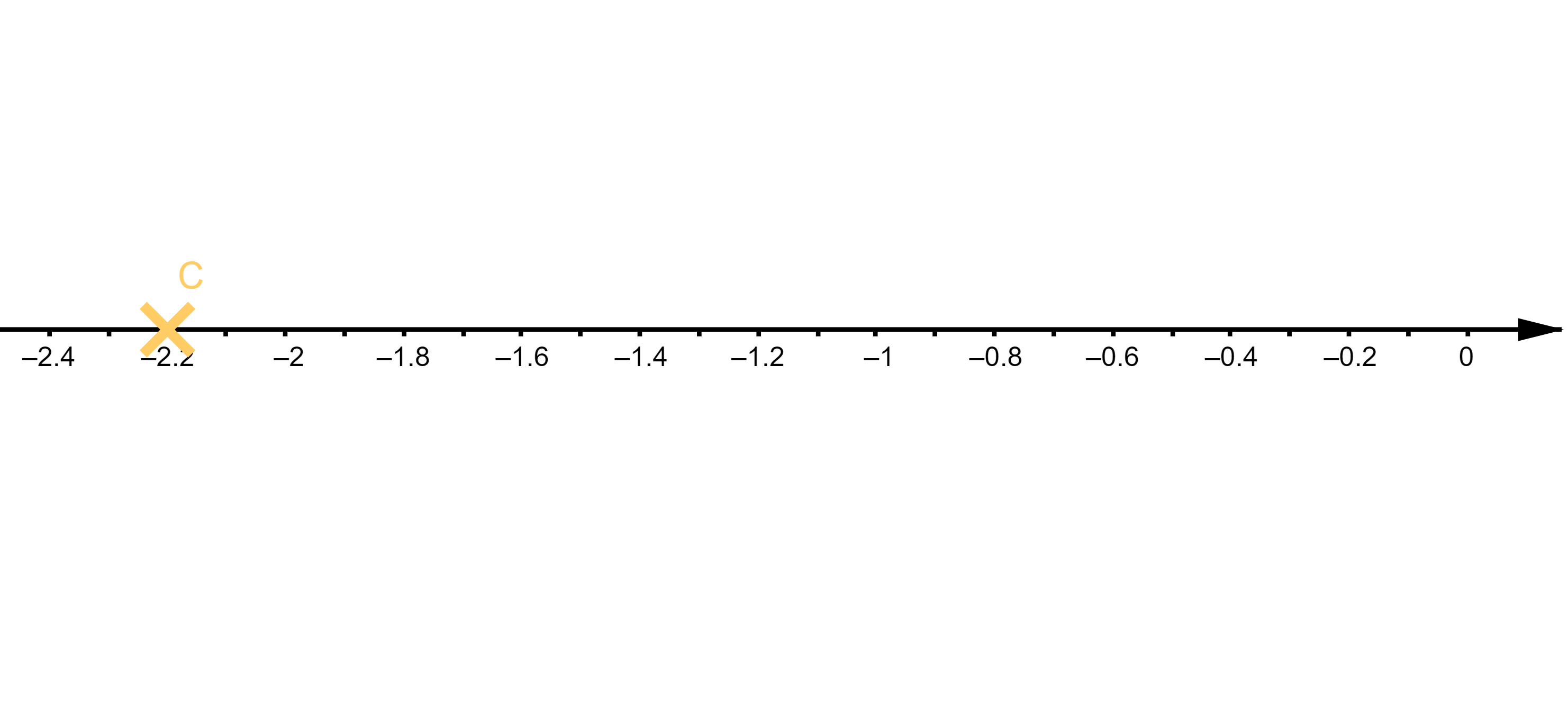
On peut lire sur le graphique que l'écriture décimale de $C$ est $C(-2,2)$.
Il s'agit maintenant de déterminer l'écriture fractionnaire la plus simplifiée pour ce point.
Attention : lors du passage d'une écriture décimale à une écriture fractionnaire, le signe ne change jamais.
Pour faciliter le passage à une écriture fractionnaire, on peut écrire $C$ de la manière suivante : $C(-\dfrac{2,2}{1})$
Ensuite on multiplie le numérateur et le dénominateur par $10$ pour que le numérateur devienne un entier relatif.
On a : $-\dfrac{2,2}{1} = -\dfrac{2,2 \times 10}{1 \times 10} = -\dfrac{22}{10}$.
Donc une écriture fractionnaire possible de $C$ est $C(-\dfrac{22}{10})$. Mais est-ce la plus simplifiée ? Ici, le numérateur est le dénominateur sont tous deux pairs, ce qui signifie qu'on peut encore simplifier l'écriture de $C$. En effet :
$-\dfrac{22}{10} = -\dfrac{11 \times 2}{5 \times 2} = -\dfrac{11}{5}$
On ne peut plus simplifier cette fraction. Donc l'écriture fractionnaire la plus simplifiée de $C$ est $C(-\dfrac{11}{5})$.
Attention : dans le passage entre deux écritures (décimale et fractionnaire) le signe d'un nombre ne change jamais.
Attention : dans une écriture fractionnaire, si le numérateur et le dénominateur sont tous deux pairs, cela signifie que l'écriture peut encore être simplifiée !
Question 4
Comme dans la question précédente, donner l'écriture décimale puis l'écriture fractionnaire la plus simplifiée du point $D$
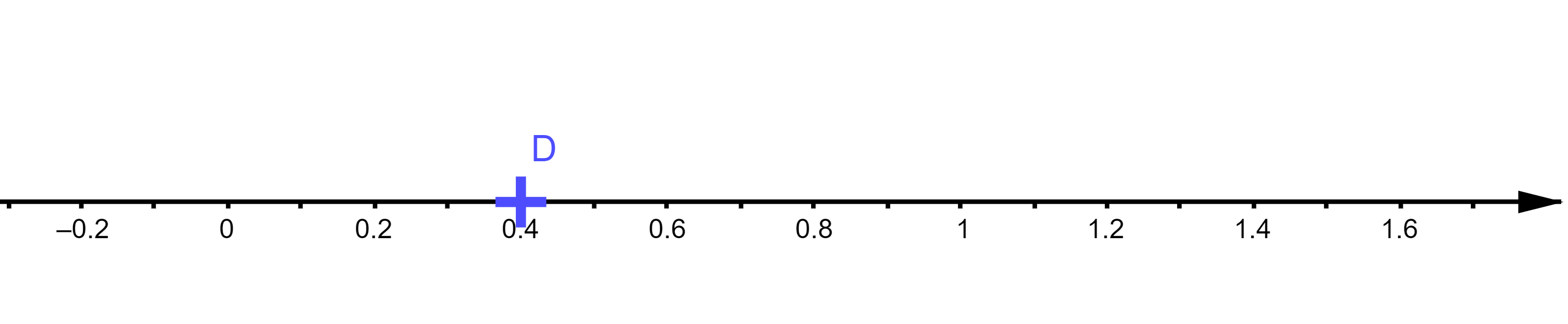
On peut lire sur le graphique que l'écriture décimale de $D$ est $D(0,4)$.
On cherche son écriture fractionnaire. Il s'agit de changer le numérateur et le dénominateur de la fraction $\dfrac{0,4}{1}$ pour que le numérateur soit un entier relatif.
On multiplie les deux par $10$. On obtient : $\dfrac{0,4}{1} = \dfrac{4}{10}$. Donc une écriture fractionnaire possible pour $D$ est $D(\dfrac{4}{10})$.
Mais $4$ et $10$ étant deux entiers pairs, l'écriture fractionnaire n'est pas la plus simplifiée possible pour $D$. On peut encore simplifier par $2$. On obtient la plus petite écriture fractionnaire pour $D$, qui est $D(\dfrac{2}{5})$
Question 5
BONUS
Quelle distance sépare les points $C$ et $D$ ?
Si on va du point $D$ au point $C$, le calcul est : $0,4 - (-2,2) = 0,4 + 2,2 = 2,6$.
En écriture décimale, la distance entre $C$ et $D$ est de $2,6$.
En écriture fractionnaire, on a $2,6 = \dfrac{2,6}{1} = \dfrac{2,6 \times 10}{1 \times 10} = \dfrac{26}{10}$.
Donc une écriture fractionnaire possible à cette distance est $=\dfrac{26}{10}=\dfrac{13}{5}$
Attention une distance est toujours positive !
$-(-1) = 1$.