L'énoncé
Répondre aux questions suivantes par rapport aux parallélogrammes particuliers.
Question 1
ABCD est un rectangle. D'après le codage de la figure, comment pouvez dire que ABCD est un carré ?

Une propriété dit qu'un rectangle dont les diagonales sont perpendiculaires est un carré.
Or, les diagonales de $ABCD$ sont perpendiculaires. Il s'agit donc bien d'un carré.
Que dire des diagonales de $ABCD$ ?
Question 2
$FIHG$ est un quadrilatère conçu à main levée. En remarquant la mesure des angles, que pouvez vous en déduire ?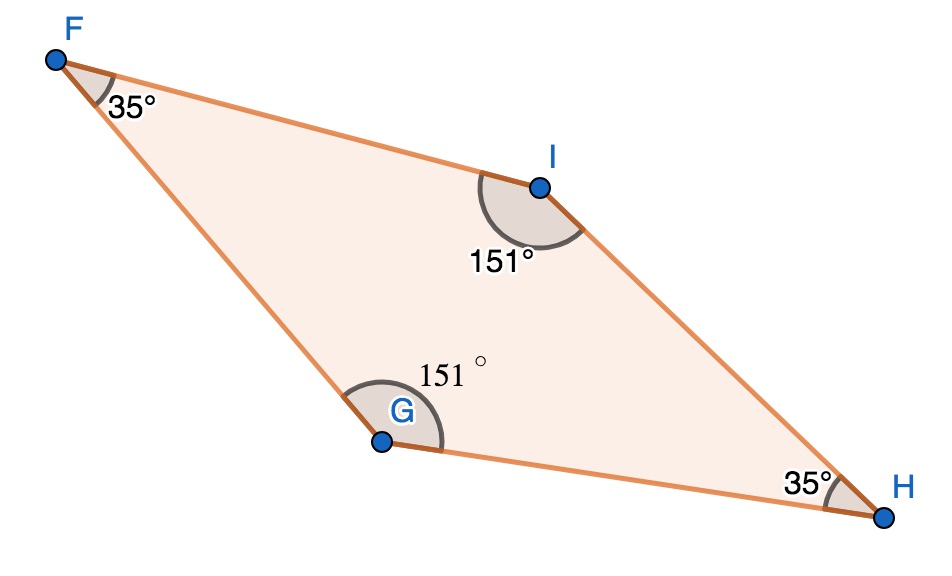
Un quadrilatère dont les angles opposés sont de même mesure est un parallélogramme.
Or, $\widehat{FIH}=\widehat{FGH}=151^{\circ}$
et $\widehat{IHG}=\widehat{GFI}=35^{\circ}$
Donc, on en conclut que $FIHG$ est un parallélogramme.
Que remarquer des angles opposés ?
Question 3
$JMLK$ est un quadrilatère. À l'aide des indications suivantes et de la figure, prouver qu'il s'agit d'un losange.
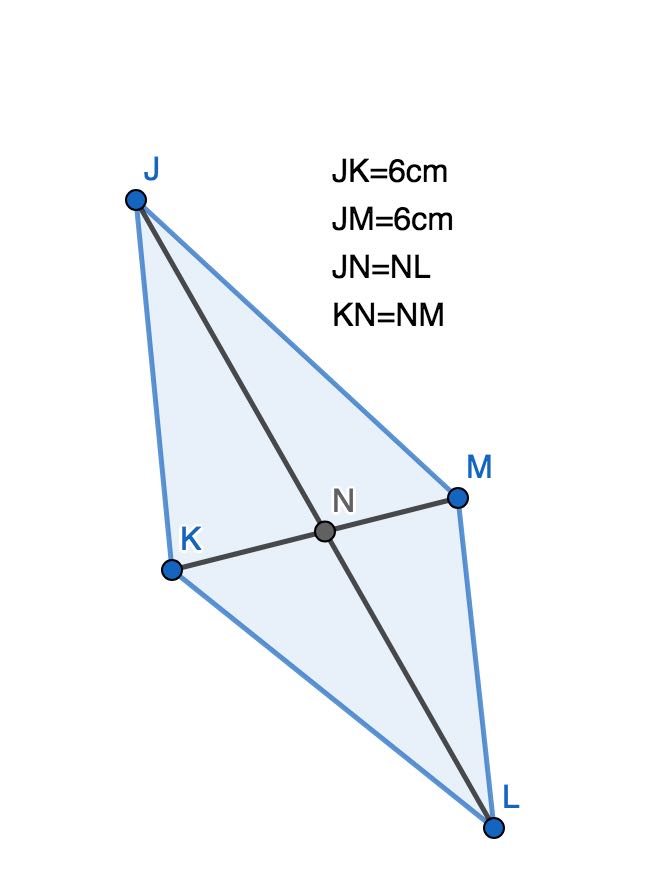
On cherche dans un premier temps, à prouver que $JMLK$ est un parallélogramme.
D'après les indications $JN=NL$ donc $N$ est le milieu de la diagonale $[JL]$
De même$ KN=NM$ donc $N$ est le milieu de la diagonale $[KM]$
Donc les diagonales du quadrilatère se coupent en leur milieu.
Or un quadrilatère dont les diagonales se coupent en leur milieu est un parallélogramme.
Donc $JMLK$ est un parallélogramme.
Ensuite, on remarque que $JK=JM=6$cm. $JK$ et $JM$ sont deux côtés consécutifs.
Or, un parallélogramme ayant deux côtés consécutifs égaux est un losange, donc $JMLK$ est un losange.
On cherche dans un premier temps, à prouver que $JMLK$ est un parallélogramme.
Question 4
Que dire d'un quadrilatère non croisé avec un centre de symétrie ?
Un quadrilatère non croisé avec un centre de symétrie est un parallélogramme. C'est une propriété de cours.
Noter qu'il ne faut pas confondre quadrilatère croisé et non croisé.
Question 5
Vous êtes sur un logiciel vous permettant de tracer des figures géométrique. Vous tracez ce losange RQPO.
Que changer au niveau de l'angle $\widehat{POR}$ pur que RQPO soit un carré ?
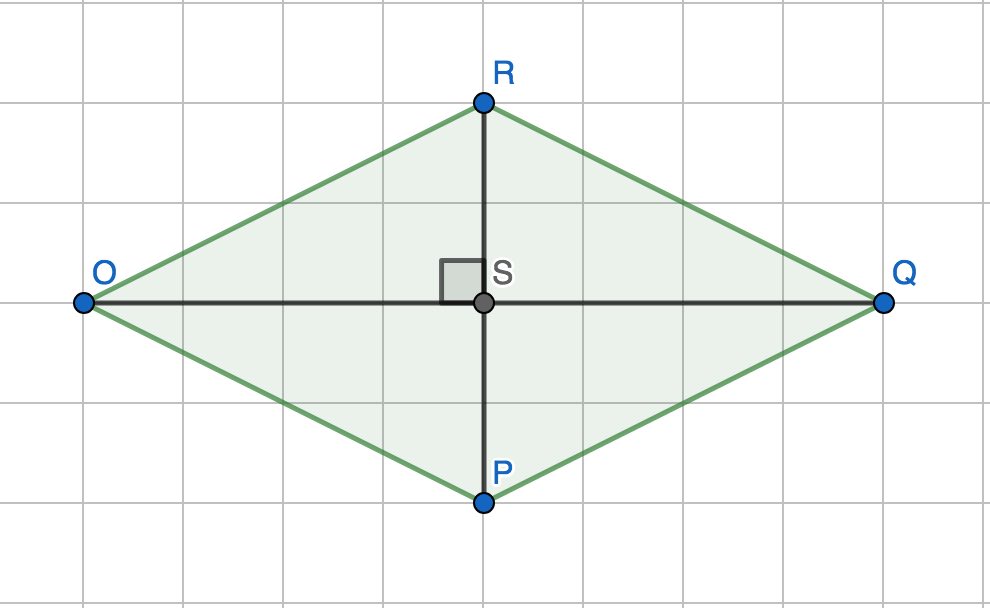
Un losange dont deux côtés sont perpendiculaires est un carré. C'est une propriété de cours.
On retient qu'il faut que $\widehat{POR}$ soit un angle droit pour que $RQPO$ soit un carré.
On change donc la valeur de $\widehat{POR}$ tel que $\widehat{POR}=90^{\circ}$.
Penser de manière inverse : comment sont les angles d'un carré ?
