Cours Parallélogrammes particuliers
lesbonsprofs.com
Image
Cours Parallélogrammes particuliers
1
Video Parallélogrammes particuliers
2
Exercice QCM -parallélogrammes particuliers
3
Exercice Exercice - Parallélogrammes particuliers
QCM
  • 1
  • 2
  • 3
  • 4
  • 5

L'énoncé

Cocher la ou les bonnes réponses.

Tu as obtenu le score de

Question 1

Que peut-on dire de ce quadrilatère conçu à main levée, en s'aidant du codage ?

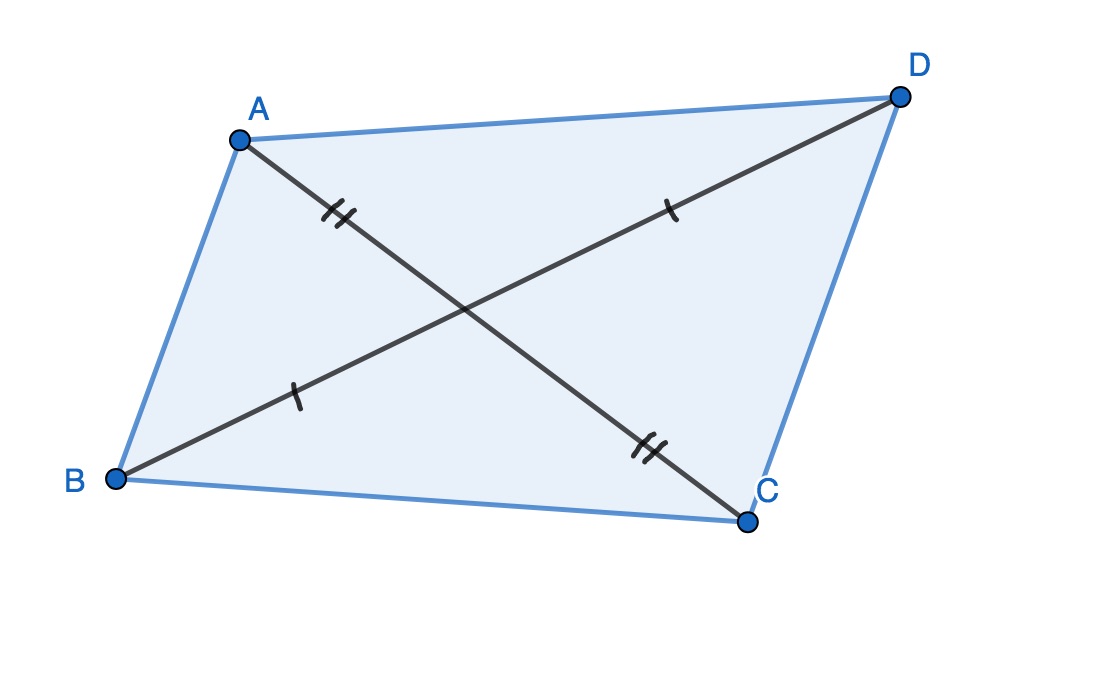
par1_1

C'est un quadrilatère quelconque.

C'est un parallélogramme.

C'est un losange.

C'est un rectangle.

$[AC]$ et $[BD]$ se coupent en leur milieu

Une propriété dit :

Si les diagonales d'un quadrilatère se coupent en leur milieu, alors c'est un parallélogramme.
Or, $ABCD$ est un quadrilatère et d'après le codage, $[AC]$ et $[BD]$ se coupent en leur milieu.

$ABCD$ est donc un parallélogramme.

 

Question 2

 Que peut on dire d'un parallélogramme qui est à la fois un losange et un rectangle ?

 (Faire une figure)

C'est un losange.

C'est un parallélogramme.

C'est un rectangle.

C'est un carré.

C'est une propriété de cours !

Un parallélogramme qui est à la fois un losange et un rectangle est un carré. C'est une propriété de cours.

Question 3

Que peut-on dire du rectangle $GHEF$ d'après le codage ?

par3

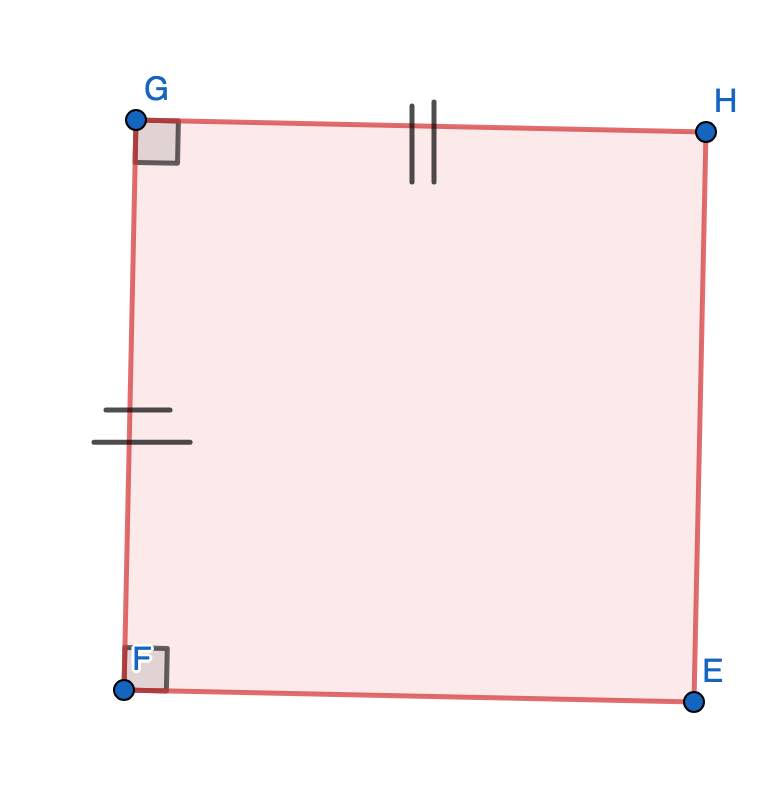
C'est un parallélogramme.

On ne peut rien en déduire.

C'est un quadrilatère.

C'est un carré.

$GH=GF$

Un rectangle est un parallélogramme. Un parallélogramme est un quadrilatère.
Ce qui nous intéresse surtout ici c'est que $GHEF$ est un rectangle et que $GH=GF$.

Or, une propriété du cours  dit que 

Un rectangle qui a deux côtés consécutifs égaux est un carré.

Donc on en déduit que $GHEF$ est un carré.

 

 

Question 4

Que peut-on dire de ce quadrilatère d'après le codage de la figure ?

par4

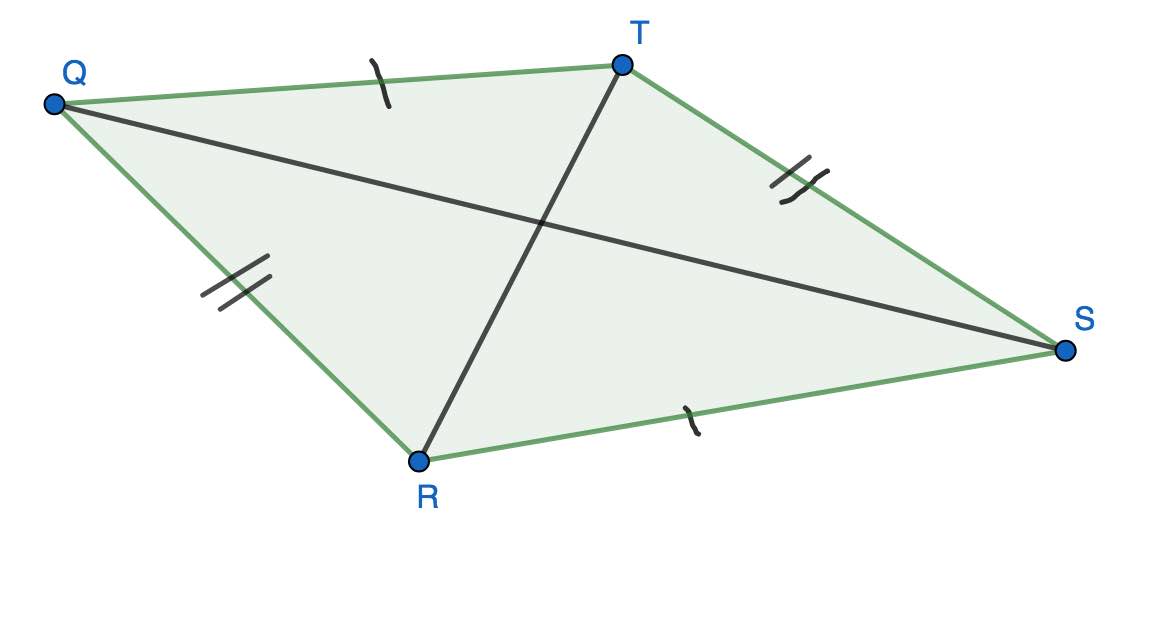
C'est un parallélogramme.

C'est un carré.

C'est un rectangle

C'est un losange

$QT=SR$ et $TS=RQ$

Si un quadrilatère non croisé a ses côtés opposés de même longueur, alors c'est un parallélogramme.
Or, $QTSR$ est un quadrilatère et $QT=SR$ et $TS=RQ$ donc $QTSR$ est un parallélogramme. 
On ne peut pas savoir si il s'agit d'un rectangle, d'un losange ou d'un carré.

 

Question 5

Que peut on dire de cette figure d'après le codage ?

par5

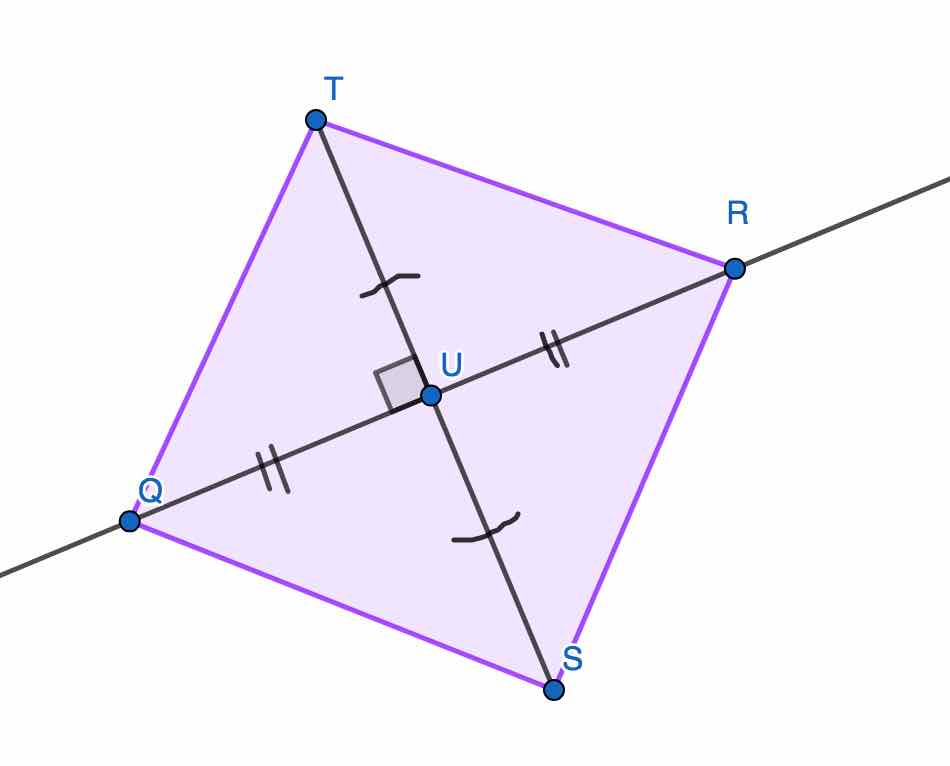
C'est un quadrilatère.

C'est un parallélogramme.

C'est un rectangle.

C'est un losange.

$TU=US$ et $RU=UQ$

$TRSQ$ est un quadrilatère dont les diagonales se coupent en leur milieu car $TU=US$ et $RU=UQ$.

On en déduit d'après la propriété du cours que $TRSQ$ est un parallélogramme.

$TRSQ$ est un parallélogramme dont les diagonales sont perpendiculaires.

Or un parallélogramme dont les diagonales sont perpendiculaires est un losange. Donc $TRSQ$ est un losange.