L'énoncé
Répondre aux cinq questions posées.
Question 1
Compléter la phrase :
Deux angles formés par deux droites coupées par une sécante sont dits alternes-internes si :
Deux angles formés par deux droites coupées par une sécante sont dits alternes-internes si :
- ils sont situés de part et d'autre de la sécante
- ils sont situés entre les deux droites
- ils ne sont pas adjacents.
Question 2
Dans le cas de deux droites non parallèles coupées par une sécante, que peut-on dire des angles alternes-internes correspondants ?
Si les deux droites ne sont pas parallèles, les deux angles alternes-internes ne sont pas égaux.
Question 3
Si les deux droites coupées par une sécante sont parallèles, que peut-on dire des angles alternes-internes correspondants ?
Si les deux droites sont parallèles, les deux angles alternes-internes sont égaux.
Question 4
Ces angles sont-ils alternes-internes, alternes-internes égaux ou sont-ils non alternes-internes ?
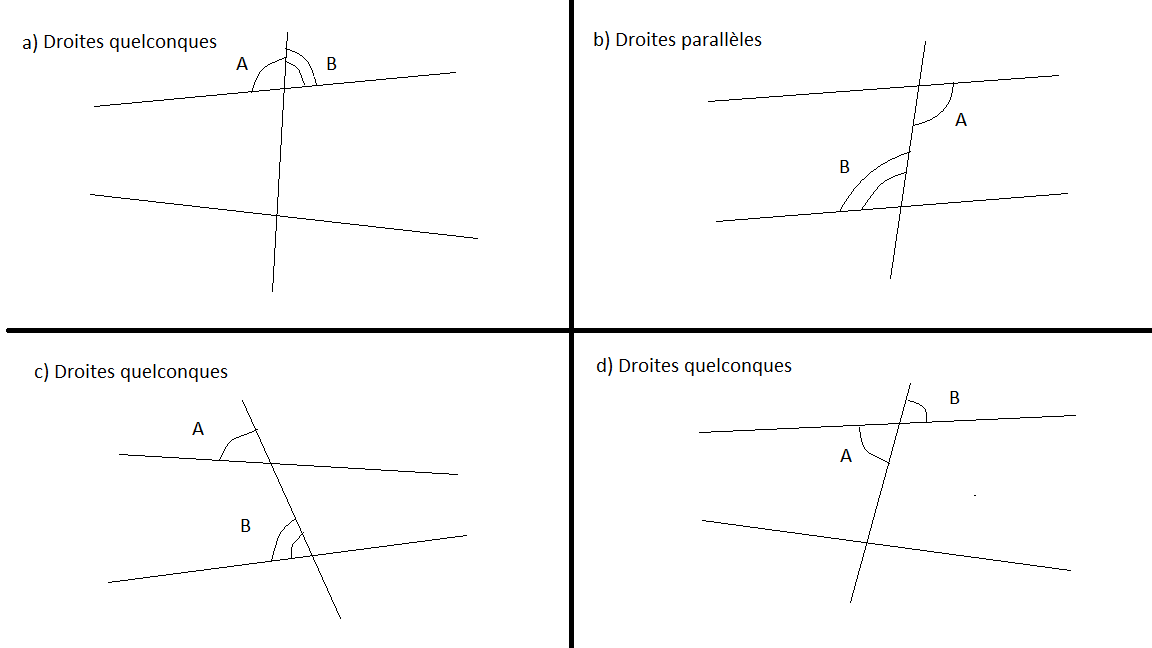
a) Ces angles ne sont pas alternes-internes (ils sont adjacents).
b) Ces angles sont alternes-internes égaux (car les droites sont parallèles).
c) Ces angles ne sont pas alternes-internes (ils sont complémentaires).
d) Ces angles ne sont pas alternes-internes (ils sont opposés par le sommet).
Question 5
Parmi tous ces angles, lesquels sont alternes-internes ?
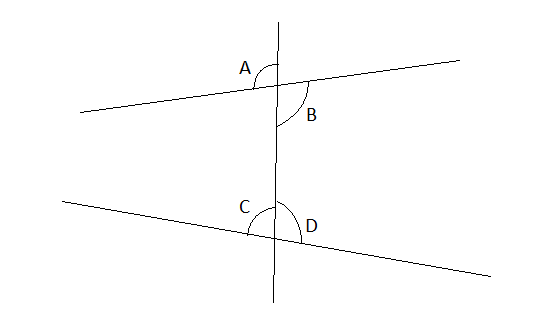
Les angles $\widehat{B}$ et$\widehat{C}$ sont alternes-internes.
