L'énoncé
Cocher la bonne réponse.
Tu as obtenu le score de
Question 1
Deux angles formés par deux droites $d$ et $d'$ coupées par une sécante $j$ sont alternes-internes si :
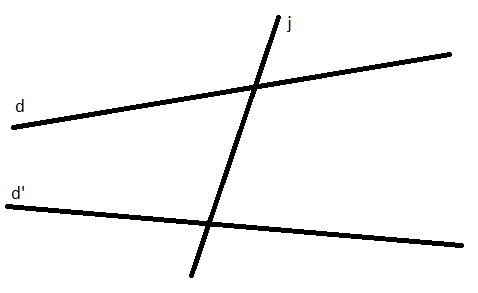
Ils sont situés de part et d'autre de la sécante.

Ils sont situés du même côté de la sécante.

Deux angles alternes-internes doivent être d'un côté et de l'autre de la sécante, pas du même côté.
Question 2
Deux angles formés par deux droites $d$ et $d'$ coupées par une sécante $j$ sont alternes-internes si :

Ils ne sont pas situés entre les deux droites.

Ils sont situés entre les deux droites.

Deux angles alternes-internes sont situés à l'intérieur des deux droites, soit entre les deux droites, et non à l'extérieur.
Question 3
Deux angles formés par deux droites $d$ et $d'$ coupées par une sécante $j$ sont alternes-internes si :

Ils sont adjacents (c'est-à-dire qu'ils ont un même sommet, un côté commun, et qu'ils sont situés de part et d'autre de ce côté commun).

Ils ne sont pas adjacents.

Deux angles alternes-internes ne doivent pas être côte à côte.
Question 4
Ces deux angles $\widehat{A}$ et $\widehat{B}$ sont-ils alternes-internes ?

Oui.
Non.
Ces angles sont alternes-internes car ils ne sont pas côte à côte, ils sont chacun d'un coté de la sécante et à l'intérieur des deux droites.
Question 5
Ces deux angles $\widehat{A}$ et $\widehat{B}$ sont-ils alternes-internes ?
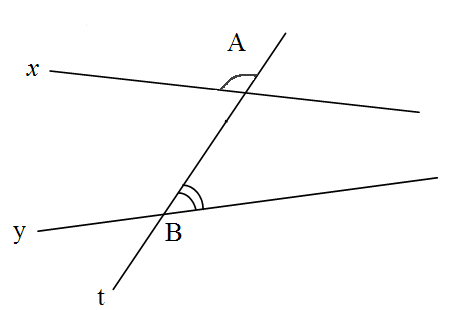
Oui.
Non.
Ces angles ne sont pas alternes-internes car même s'ils ne sont pas côte à côte et chacun d'un coté de la sécante, un des deux angles n'est pas à l'intérieur des deux droites.
