L'énoncé
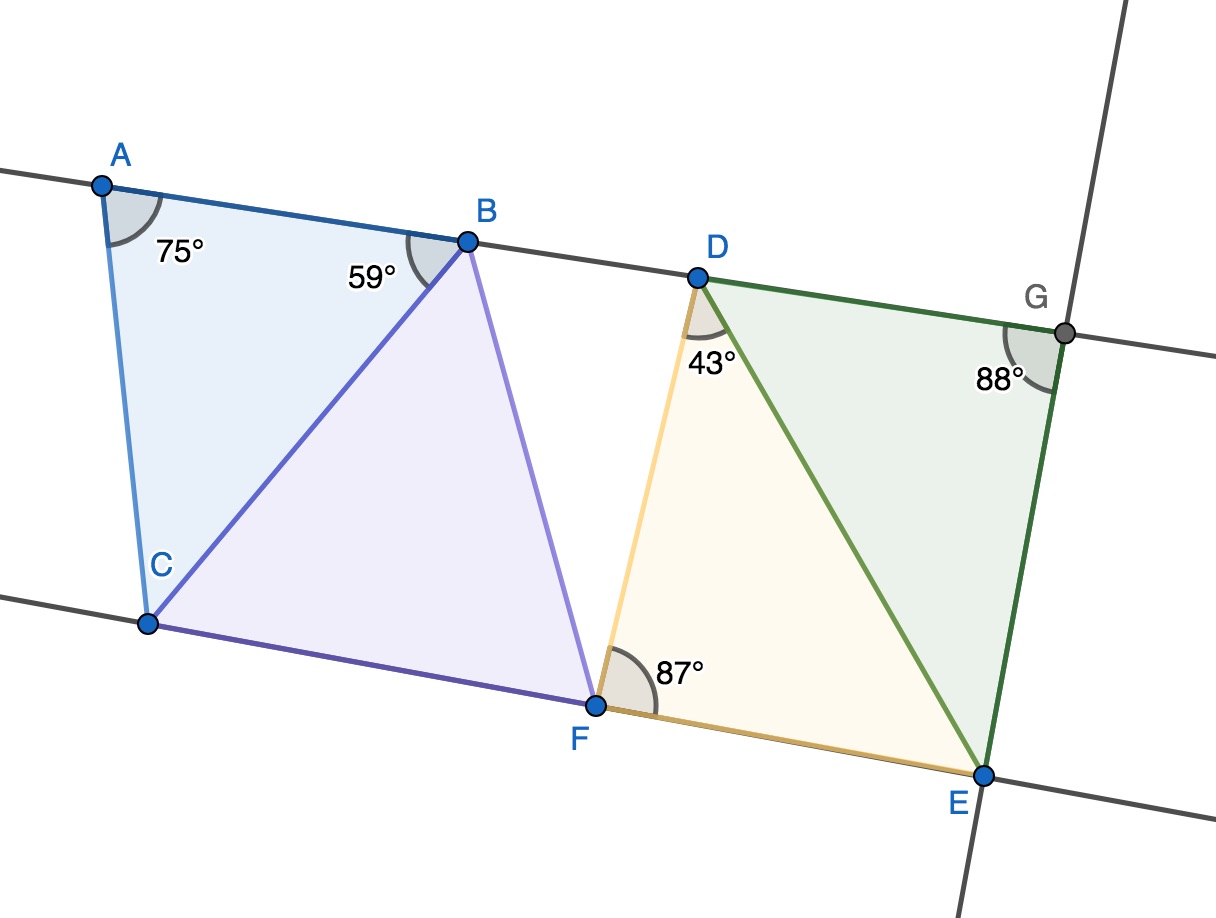
Répondre aux questions en vous aidant de la figure suivante.
Noter que la droite (FE) est perpendiculaire à (GE).
Noter aussi que le triangle BCF est équilatéral.
Question 1
Que mesure l'angle $\widehat{ACB}$ ?
La somme des mesures des angles d'un triangle vaut $180^\circ$.
On peut donc écrire : $\widehat{ACB}$=$180^\circ-\widehat{ABC}-\widehat{CAB}\\=180^\circ-59^\circ-75^\circ\\=46^\circ$
La somme des mesures des angles d'un triangle vaut $180^\circ$.
Question 2
Que mesure l'angle $\widehat{DEF}$ ?
La somme des mesures des angles d'un triangle vaut $180^\circ$.
On peut donc écrire : $\widehat{DEF}$=$180^\circ-\widehat{EFD}-\widehat{FDE}\\=180^\circ-87^\circ-43^\circ\\=50^\circ$
La somme des mesures des angles d'un triangle vaut $180^\circ$.
Question 3
Que mesurent les 3 angles du triangle $BCF$ ?
Les 3 angles du triangles $BCF$ mesurent $60^\circ$ car il est équilatéral. C'est une propriété du cours.
$BCF$ est équilatéral.
Question 4
Que mesure l'angle $\widehat{DEG}$ ?
L'angle $\widehat{FEG}$ mesure $90^\circ$ car (FE) et (GE) sont perpendiculaires.
Se rappeler que l'angle $\widehat{FED}=50^\circ$ d'après la question 2.
Or, $\widehat{FEG}$=$\widehat{FED}+\widehat{DEG}$.
Donc $\widehat{DEG}=\widehat{FEG}-\widehat{FED}\\=90^\circ-50^\circ=40^\circ$
$(FE)$ et $(GE)$ sont perpendiculaires
Question 5
Que mesure l'angle $\widehat{EDG}$ ?
La somme des mesures des angles d'un triangle vaut $180^\circ$.
On peut donc écrire : $\widehat{EDG}$=$180^\circ-\widehat{DGE}-\widehat{GED}\\=180^\circ-88^\circ-40^\circ\\=52^\circ$
La somme des mesures des angles d'un triangle vaut $180^\circ$
